题目内容
20.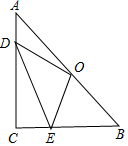 在Rt△ABC中,点O为斜边AB的中点,D、E分别在边AC、BC上,若CB=6,CA=8,高CH=$\frac{24}{5}$,则OD+DE+EO的最小值为10.
在Rt△ABC中,点O为斜边AB的中点,D、E分别在边AC、BC上,若CB=6,CA=8,高CH=$\frac{24}{5}$,则OD+DE+EO的最小值为10.
分析 如图,作点O关于AC的对称点O′,点O关于BC的对称点O″,连接O′O″.因为△ODE的周长=OD+DE+OE=O′D+DE+EO″,根据两点直径线段最短,可知当O′、D、E、O″共线时,△ODE的周长最小,最小值为O′O″,求出O′O″即可.
解答 解:如图,作点O关于AC的对称点O′,点O关于BC的对称点O″,连接O′O″.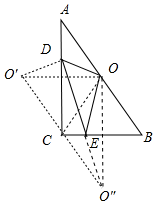
∵△ODE的周长=OD+DE+OE=O′D+DE+EO″,
根据两点直径线段最短,可知当O′、D、E、O″共线时,△ODE的周长最小,最小值为O′O″,
∵∠ACB=90°,AC=8,BC=6,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,根据对称性可知,O′、C、O″共线,
∵AO=OB,
∴OC=$\frac{1}{2}$AB=5,
∴O′O″=2OC=10.
∴OD+DE+EO的最小值为10,
故答案为10.
点评 本题考查轴对称-最短问题、勾股定理、直角三角形斜边中线性质等知识,解题的关键是学会利用对称解决最短问题,属于中考常考题型.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
10.对于函数y=-x2+2x-2,使得y随x的增大而增大的x的取值范围是( )
| A. | x>1 | B. | x≥0 | C. | x≤0 | D. | x<1 |
11.在△ABC中,∠A=30°,∠B=50°,则∠C为( )
| A. | 30° | B. | 50° | C. | 80° | D. | 100° |
8.下列说法正确的是( )
| A. | 半圆是弧,弧也是半圆 | B. | 三点确定一个圆 | ||
| C. | 平分弦的直径垂直于弦 | D. | 直径是同一圆中最长的弦 |
15.从一副54张的扑克牌中任意抽一张,以下事件中可能性最大的是( )
| A. | 抽到方块8 | B. | 抽到K牌 | C. | 抽到梅花 | D. | 抽到大王 |
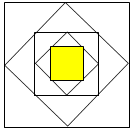 如图,把一个正方形各边中点连结起来组成第二个正方形,再把第二个正方形各边的中点连结起来组成第三个正方形,按照这样的方法连结得到的第五个正方形的面积占第一个正方形面积的$\frac{1}{16}$.(填几分之几)
如图,把一个正方形各边中点连结起来组成第二个正方形,再把第二个正方形各边的中点连结起来组成第三个正方形,按照这样的方法连结得到的第五个正方形的面积占第一个正方形面积的$\frac{1}{16}$.(填几分之几)