题目内容
已知抛物线
．
（1）求证：该抛物线与
轴一定有两个交点；
（2）若该抛物线与轴的两个交点分别为A、B，且它的顶点为P，求△ABP的面积。
（1）证明见解析；（2）27.
【解析】
试题分析：根据b2-4ac与零的关系即可判断出二次函数y=x2-2x-8的图象与x轴交点的个数．
试题解析：（1）解方程x2-2x-8=0，得x1=-2，x2=4．
故抛物线y=x2-2x-8与x轴有两个交点．
（2）由（1）得A（-2，0），B（4，0），故AB=6．
由y=x2-2x-8=x2-2x+1-9=（x-1）2-9，
故P点坐标为（1，-9）；
过P作PC⊥x轴于C，则PC=9，
∴S△ABP=
AB•PC=×6×9=27．
考点：抛物线与x轴的交点．
练习册系列答案
相关题目
与一次函数
的图象在第一象限相交于点A（1，
）
的图象的对称轴是（ ）
=－2 B．直线
=2 C．直线
（米）与水平距离
（米）之间的关系是
，则铅球推出距离 米．
（单位：米）与车速
（单位：米/秒）之间有如下关系：
，其中
为司机的反应时间（单位：秒），
为制动系数．某机构为测试司机饮酒后刹车距离的变化，对某种型号的汽车进行了“醉汉”驾车测试，已知该型号汽车的制动系数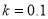
，并测得志愿者在未饮酒时的反应时间
秒．