题目内容
已知（a2+b2）2-4（a2+b2）+4+y2-6y+9=0，且a，b，y都是正整数，求（a+b+y）2的值．
考点：配方法的应用,非负数的性质：偶次方
专题：
分析：由（a2+b2）2-4（a2+b2）+4+y2-6y+9=0可得（a2+b2-2）2+（y-3）2=0，可得a2+b2=2，y=3，再根据都是正整数可求得a=b=1，代入计算求值．
解答：解：∵（a2+b2）2-4（a2+b2）+4+y2-6y+9=0，
∴（a2+b2-2）2+（y-3）2=0，
∴a2+b2=2，y=3，
∵a，b都是正整数，
∴a=b=1，
∴a+b+y=5，
∴（a+b+y）2=25．
∴（a2+b2-2）2+（y-3）2=0，
∴a2+b2=2，y=3，
∵a，b都是正整数，
∴a=b=1，
∴a+b+y=5，
∴（a+b+y）2=25．
点评：本题主要考查配方法及非负数的性质的应用，把a2+b2看成一个整体是解题的关键．
练习册系列答案
相关题目
交AE的延长线于点D，CG平分∠ACB交AD于点G，CF⊥AD交AB于F，求证：BF=CG；CF=2DE．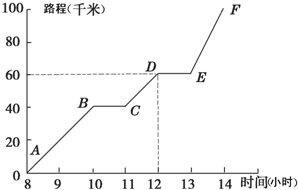
如图，描述了小明早晨8时到下午14时，骑摩托车从甲地到乙地所走路程与时间的关系，根据折线图提供的信息思考下列问题：?