题目内容
已知a、b、c是△ABC三边长,且满足a2+b2+bc=ac+2ab,试判断△ABC的形状.
考点:因式分解的应用
专题:
分析:将所给的等式移项,运用分组分解法将等式的左边因式分解,借助三角形的三边关系问题即可解决.
解答:解:∵a2+b2+bc=ac+2ab,
∴a2+b2+bc-ac-2ab=0,
即(a-b)2-c(a-b)=0,
∴(a-b)(a-b-c)=0;
∵a-b-c<0,
∴a-b=0,
即a=b,
∴△ABC是等腰三角形.
∴a2+b2+bc-ac-2ab=0,
即(a-b)2-c(a-b)=0,
∴(a-b)(a-b-c)=0;
∵a-b-c<0,
∴a-b=0,
即a=b,
∴△ABC是等腰三角形.
点评:该命题主要考查了因式分解的应用问题;解题的关键是运用因式分解,灵活将所给的等式恒等变形,进而分析、判断或证明.

练习册系列答案
相关题目
 在排成每行七天的日历表中取下一个3×3方块(如图),若所有日期数之和为135,则n的值为( )
在排成每行七天的日历表中取下一个3×3方块(如图),若所有日期数之和为135,则n的值为( )| A、13 | B、14 | C、15 | D、9 |
 已知:在△ABC中,∠B=40°,∠C=20°,AD⊥AC交BC于点D,求证:CD=2AB.
已知:在△ABC中,∠B=40°,∠C=20°,AD⊥AC交BC于点D,求证:CD=2AB.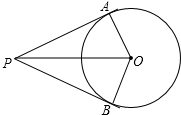 如图,一点P在⊙O外,PA,PB是⊙O的两条切线,切点为A,B,∠APB=60°,AP=3cm,则圆的半径等于
如图,一点P在⊙O外,PA,PB是⊙O的两条切线,切点为A,B,∠APB=60°,AP=3cm,则圆的半径等于