题目内容
如图，能判断直线AB∥CD的条件是（ ）| A、∠1=∠2 |
| B、∠3=∠4 |
| C、∠1+∠3=180° |
| D、∠3+∠4=180° |
考点：平行线的判定
专题：计算题
分析：根据平行线的判定得∠4=∠5时，AB∥CD，由于∠3+∠5=180°，所以∠3+∠4=180°时，AB∥CD．
解答：
解：∵∠3+∠5=180°，
而当∠4=∠5时，AB∥CD，
当∠3+∠4=180°，
而∠3+∠5=180°，
所以∠4=∠5，则AB∥CD．
故选D．
解：∵∠3+∠5=180°，而当∠4=∠5时，AB∥CD，
当∠3+∠4=180°，
而∠3+∠5=180°，
所以∠4=∠5，则AB∥CD．
故选D．
点评：本题考查了平行线的判定：同位角相等，两直线平行．
练习册系列答案
相关题目
在Rt△OAB中，∠AOB=90°，OA=3，OB=4，以点O为圆心，半径为5作圆，则斜边AB所在的直线⊙O的位置关系是（ ）
| A、相交 | B、相切 |
| C、相离 | D、无法确定 |
下列说法中正确的是（ ）
| A、图形平移是指把图形沿水平方向移动 |
| B、“相等的角是对顶角”是一个真命题 |
| C、平移前后的形状和大小都没有发生改变 |
| D、“直角都相等”是一个假命题 |
下列算式能用平方差公式计算的是（ ）
| A、（2a+b）（2b-a） | ||||
B、(
| ||||
| C、（3x-y）（-3x+y） | ||||
| D、（-a-b）（-a+b） |
下列是一元一次方程的是（ ）
| A、x+3y=9 | ||
| B、3xy=6 | ||
C、
| ||
| D、5x+6=3 |
若a2=25，|b|=3，则a+b所有可能的值为（ ）
| A、8 | B、8或2 |
| C、8或-2 | D、±8或±2 |
已知⊙O与直线l相切于A点，点P、Q同时从A点出发，P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动，当Q运动到点A时，点P也停止运动．连接OQ、OP（如图），则阴影部分面积S1、S2的大小关系是（ ）| A、S1=S2 |
| B、S1≤S2 |
| C、S1≥S2 |
| D、先S1＜S2，再S1=S2，最后S1＞S2 |
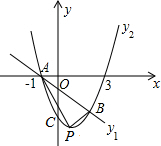已知一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象交于两点A（-1，0）、B（2，-3），且二次函数与y轴交于点C，P为抛物线顶点．求△ABP的面积．