题目内容
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.

(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,(1)中的结论②还成立吗?若成立,请给予证明;若不成立,线段DE、AD、BE又有怎样的数量关系?请写出你的猜想,不需证明.

(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,(1)中的结论②还成立吗?若成立,请给予证明;若不成立,线段DE、AD、BE又有怎样的数量关系?请写出你的猜想,不需证明.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)易证∠DAC=∠ECB,可证△ADC≌△CEB,可得CD=BE,即可解题;
(2)不成立,新结论为:DE=AD-BE;证明:易证∠DAC=∠ECB,可证△ADC≌△CEB,可得CD=BE,证明新结论.
(2)不成立,新结论为:DE=AD-BE;证明:易证∠DAC=∠ECB,可证△ADC≌△CEB,可得CD=BE,证明新结论.
解答:解:(1)∵∠DAC+∠ACD=90°,∠ACD+∠BCE=90°,
∴∠DAC=∠ECB,
∵在△ADC和△CEB中,
,
∴△ADC≌△CEB,(AAS)
∴CD=BE,AD=CE
∵DE=CE+CE,
∴DE=AD+BE;
(2)不成立,新结论为:DE=AD-BE;
证明:∵∠DAC+∠ACD=90°,∠ACD+∠BCE=90°,
∴∠DAC=∠ECB,
∵在△ADC和△CEB中,
,
∴△ADC≌△CEB,(AAS)
∴CD=BE,AD=CE
∵DE=CE-CD,
∴DE=AD-BE.
∴∠DAC=∠ECB,
∵在△ADC和△CEB中,
|
∴△ADC≌△CEB,(AAS)
∴CD=BE,AD=CE
∵DE=CE+CE,
∴DE=AD+BE;
(2)不成立,新结论为:DE=AD-BE;
证明:∵∠DAC+∠ACD=90°,∠ACD+∠BCE=90°,
∴∠DAC=∠ECB,
∵在△ADC和△CEB中,
|
∴△ADC≌△CEB,(AAS)
∴CD=BE,AD=CE
∵DE=CE-CD,
∴DE=AD-BE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ADC≌△CEB是解题的关键.

练习册系列答案
相关题目
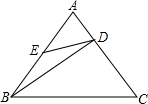 如图,正△ABC中,点E是AB的中点,点D在AC上,且DC=2DA,则( )
如图,正△ABC中,点E是AB的中点,点D在AC上,且DC=2DA,则( )| A、△AED∽△BED |
| B、△AED∽△CBD |
| C、△AED∽△ABD |
| D、△BAD∽△BCD |
下列计算:①(-1)4=-1;②(-2)4=16;③(-3)3=-9;④-24=16.其中正确的是( )
| A、①②③④ | B、②③④ |
| C、②③ | D、② |
 如图,△ABC中,点D在AB上,如果AC2=AD•AB,那么△ACD与△ABC相似吗?说说你的理由.
如图,△ABC中,点D在AB上,如果AC2=AD•AB,那么△ACD与△ABC相似吗?说说你的理由. 如图,P为△ABC的边AB、AC的垂直平分线的交点,∠BAC=50°,求∠BPC的度数.
如图,P为△ABC的边AB、AC的垂直平分线的交点,∠BAC=50°,求∠BPC的度数.