题目内容
13. 如图,直线l:y=-x+b(b>0,且b为常数)与双曲线c1:y=$\frac{1}{x}$(x>0)相交于A、B两点,与坐标轴交于C、D点,连接OA、OB,过点B、点A分别作x轴、y轴的垂线,交坐标轴于E、F两点,两垂线的交点为G,双曲线c2:y=$\frac{k}{x}$(x>0)经过点G,其中点A的坐标为A(x1,y1).则下列结论:
如图,直线l:y=-x+b(b>0,且b为常数)与双曲线c1:y=$\frac{1}{x}$(x>0)相交于A、B两点,与坐标轴交于C、D点,连接OA、OB,过点B、点A分别作x轴、y轴的垂线,交坐标轴于E、F两点,两垂线的交点为G,双曲线c2:y=$\frac{k}{x}$(x>0)经过点G,其中点A的坐标为A(x1,y1).则下列结论:①点B的坐标为B(y1,x1);
②图中全等的三角形共有3对;
③若AB=$\sqrt{2}$,则OF-AF=1;
④四边形GAOB的面积为k-1;
⑤若∠AOB=45°,则S△AOB=1.
其中正确的结论是①③④⑤(只填序号)
分析 先根据对称性直接得出①正确,②错误,再根据等腰直角三角形的性质计算得出③正确,利用双曲线的性质直接求出四边形GAOB的面积,得出④正确,最后再判断出△AOF≌△AOH,△BOH≌△BOE即可得出⑤正确.
解答 解:如图,连接OG,
根据题意,图象关于直线y=x成轴对称,
∵y=-x+b与坐标轴交于C,D,
∴C(0,b),D(b,0),且∠ACO=∠CDO=45°,
由对称性得,OE=OF,AF=BE,
A(x1,y1).
∴(y1,x1);
所以①正确;
由对称性得,△COB≌△DOA,△AFC≌△BED,△AFO≌△BEO,△AOC≌△BOD,
所以②错误;
当AB=$\sqrt{2}$时,AG=1,
∴OF-AF=FG-AF=AG=1,
所以③正确;
∴S四边形GAOB=S四边形OEGF-S△AFO-S△BOE=k-$\frac{1}{2}$-$\frac{1}{2}$=k-1,
所以④正确;
如图,连接OG,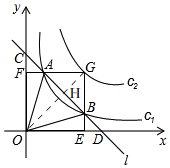
∵∠AOB=45°,
∴∠AOF=∠AOH=22.5°,
在△AOF和△AOH中,$\left\{\begin{array}{l}{∠AOF=∠AOH}\\{∠AFO=∠AHO}\\{OA=OA}\end{array}\right.$,
∴△AOF≌△AOH,
同理:△BOH≌△BOE,
∴S△AOB=2S△AOH=1,
所以⑤正确;
故答案为:①③④⑤.
点评 此题是反比例函数综合题,主要考查了反比例函数的性质,全等三角形的性质和判定,反比例函数中k的几何意义,反比例函数图形上的一点和坐标轴围成的矩形的面积,本题中对称性的应用是解本题的关键.

练习册系列答案
相关题目
2.某校举办初中生演讲比赛,每班派两名学生参赛,现某班有A、B、C三名学生竞选,他们的笔试成绩和口试成绩(单位:分)分别用两种方式进行了统计,如表和图(1):

(1)m=90,并将图(1)补充完整;
(2)竞选的最后一个程序是由本校的300名学生代表进行投票,每票计1分,三名候选人的得分情况如图(2)(没有弃权票,每名学生只能推荐一人);
①若将笔试、口试、得票三项测试得分按4:3:3的比例确定最后成绩,请计算学生A的最后成绩;
②若A、B、C三名学生中有一名男生,两名女生,选其中两名学生参赛,求恰好选中一男一女的概率.(要求用树状图或列表法写出分析过程)
| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 口试 | m | 80 | 85 |

(1)m=90,并将图(1)补充完整;
(2)竞选的最后一个程序是由本校的300名学生代表进行投票,每票计1分,三名候选人的得分情况如图(2)(没有弃权票,每名学生只能推荐一人);
①若将笔试、口试、得票三项测试得分按4:3:3的比例确定最后成绩,请计算学生A的最后成绩;
②若A、B、C三名学生中有一名男生,两名女生,选其中两名学生参赛,求恰好选中一男一女的概率.(要求用树状图或列表法写出分析过程)
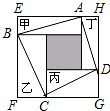 如图所示,甲、乙、丙、丁四个长方形拼成正方形EFGH,中间阴影为正方形.已知甲、乙、丙、丁四个长方形面积的和是48cm2,四边形ABCD的面积是40cm2,则甲、乙、丙、丁四个长方形周长的总和为64cm.
如图所示,甲、乙、丙、丁四个长方形拼成正方形EFGH,中间阴影为正方形.已知甲、乙、丙、丁四个长方形面积的和是48cm2,四边形ABCD的面积是40cm2,则甲、乙、丙、丁四个长方形周长的总和为64cm. 如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠EBC=32°,∠AEB=70°.
如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠EBC=32°,∠AEB=70°. 把下列各数化简后在数轴上表示出来,并把原数按从小到大的顺序用“<”号连接起来.
把下列各数化简后在数轴上表示出来,并把原数按从小到大的顺序用“<”号连接起来.