题目内容
1．
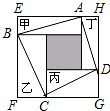如图所示，甲、乙、丙、丁四个长方形拼成正方形EFGH，中间阴影为正方形．已知甲、乙、丙、丁四个长方形面积的和是48cm2，四边形ABCD的面积是40cm2，则甲、乙、丙、丁四个长方形周长的总和为64cm．
分析 通过图片可看出，中间阴影部分的正方形的面积=四边形ABCD的面积-甲、乙、丙、丁四个长方形面积的和的一半，从而可求得中间的正方形的面积，则不难得到S正方形EFGH进面可求得正方形EFGH的边长及其周长，通过观察可发现甲乙丙丁的周长和正好是正方形EFGH周长的2倍，从而就可求得甲、乙、丙、丁四个长方形周长的总和．
解答 解：∵阴影部分的面积=40-48÷2=16（cm2），
∴S正方形EFGH=S阴影+S甲乙丙丁的面积和=16+48=64（cm2），
∴FG=8cm，
∴正方形EFGH的周长=32cm
∴甲、乙、丙、丁四个长方形周长的总和=32×2=64（cm）．
故答案为：64．
点评 此题主要考查了图形的剪拼、正方形的性质、矩形的性质以及矩形和正方形的面积和周长的计算方法等，只要把图看透，熟练运用好各知识点，便可以顺利解答．
练习册系列答案
相关题目
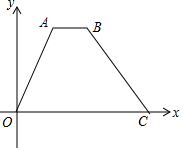如图，在平面直角坐标系中，梯形ABCD的四个顶点的坐标分别是A（2，3$\sqrt{5}$），B（4，3$\sqrt{5}$），C（10，0），D（0，0）．
如图，直线l：y=-x+b（b＞0，且b为常数）与双曲线c1：y=$\frac{1}{x}$（x＞0）相交于A、B两点，与坐标轴交于C、D点，连接OA、OB，过点B、点A分别作x轴、y轴的垂线，交坐标轴于E、F两点，两垂线的交点为G，双曲线c2：y=$\frac{k}{x}$（x＞0）经过点G，其中点A的坐标为A（x1，y1）．则下列结论：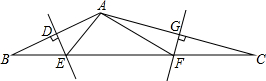
如图，在△ABC中，AB、AC的垂直平分线分别交BC于点E、F．