题目内容
15.在一幅扑克牌中取红桃、梅花、方块各一张牌混合放在一起,第一次从中任意摸出一张牌,放回洗匀,再任意摸出一张牌,请用树状图表示上述两次摸牌所有可能的结果,并求出两次恰好摸到同种花色牌的概率.分析 画树状图展示所有9种等可能的结果数,再找出两次恰好摸到同种花色牌的结果数,然后根据概率公式求解.
解答 解:画树状图为:
共有9种等可能的结果数,其中两次恰好摸到同种花色牌的结果数为3,
所以两次恰好摸到同种花色牌的概率=$\frac{3}{9}$=$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.\

练习册系列答案
相关题目
5.下列各曲线中不能表示y是x的函数是( )
| A. |  | B. |  | C. |  | D. |  |
7.中考前的模拟考试对于学生来说具有重大的指导意义,现抽取m名学生的数学一模成绩进行整理分组,形成如下表格(x代表成绩,规定x>140为优秀),并绘制出扇形统计图和频数分布直方图(横坐标表示成绩,单位:分).
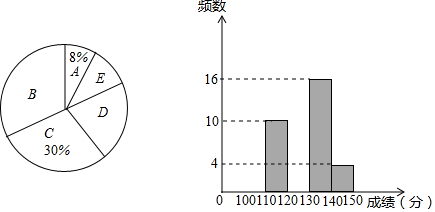
(1)m的值为50;扇形统计图中D组对应的圆心角是72°.
(2)若要从成绩优秀的学生甲、乙、丙、丁中,随机选出2人介绍经验,求甲、乙两人中至少有1人被选中的概率(通过画树状图或列表法进行分析).
| A组 | 140<x≤150 |
| B组 | 130<x≤140 |
| C组 | 120<x≤130 |
| D组 | 110<x≤120 |
| E组 | 100<x≤110 |

(1)m的值为50;扇形统计图中D组对应的圆心角是72°.
(2)若要从成绩优秀的学生甲、乙、丙、丁中,随机选出2人介绍经验,求甲、乙两人中至少有1人被选中的概率(通过画树状图或列表法进行分析).
 如图,P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足.
如图,P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足.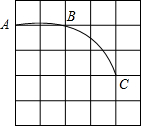 如图,在5×5的正方形网格中,每个小正方形的边长为1,一段圆弧经过格点A、B、C,请完成下列任务.
如图,在5×5的正方形网格中,每个小正方形的边长为1,一段圆弧经过格点A、B、C,请完成下列任务. 已知关于x的不等式3x+mx>-8的解集如图所示,则m的值为1.
已知关于x的不等式3x+mx>-8的解集如图所示,则m的值为1. 如图,在五边形ABCDE中,AP平分∠EAB,BP平分∠ABC.
如图,在五边形ABCDE中,AP平分∠EAB,BP平分∠ABC.