题目内容
10.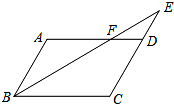 如图,在平行四边形ABCD中,点E是CD延长线上一点,BE与AD交于点F,若CD=2DE,且△DEF的面积为3,则三角形ABF的面积为( )
如图,在平行四边形ABCD中,点E是CD延长线上一点,BE与AD交于点F,若CD=2DE,且△DEF的面积为3,则三角形ABF的面积为( )| A. | 6 | B. | 8 | C. | 9 | D. | 12 |
分析 根据平行四边形的性质推出AB=CD,AB∥CD,根据相似三角形的判定得出△ABF∽△DEF,根据相似三角形的性质得出$\frac{{S}_{△DEF}}{{S}_{△ABF}}$=($\frac{DE}{AB}$)2,代入求出即可.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴△ABF∽△DEF,
∴$\frac{{S}_{△DEF}}{{S}_{△ABF}}$=($\frac{DE}{AB}$)2,
∵CD=2DE,△DEF的面积为3,
∴三角形ABF的面积为12,
故选D.
点评 本题考查了平行四边形的性质,相似三角形的性质和判定的应用,能求出$\frac{{S}_{△DEF}}{{S}_{△ABF}}$=($\frac{DE}{AB}$)2是解此题的关键,注意:相似三角形的面积之比等于相似比的平方.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
1.我国最长的河流长江全长约6300千米,6300千米用科学记数法表示为( )
| A. | 6.3×102千米 | B. | 6.3×103千米 | C. | 0.63×104千米 | D. | 630×10千米 |
 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0.其中正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0.其中正确的是( )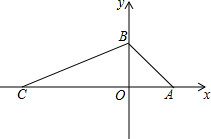 如图,在平面直角坐标系中,O为坐标原点,直线y=-x+4与x轴交于点A,与y轴交于点B,点C在x轴负半轴上,S△ABC=28.点P是线段CA上一动点.
如图,在平面直角坐标系中,O为坐标原点,直线y=-x+4与x轴交于点A,与y轴交于点B,点C在x轴负半轴上,S△ABC=28.点P是线段CA上一动点. 如图,⊙D与x轴相交于A(-2,0),B(-8,0),与y轴相切于C,则圆心D的坐标为(-5,4).
如图,⊙D与x轴相交于A(-2,0),B(-8,0),与y轴相切于C,则圆心D的坐标为(-5,4).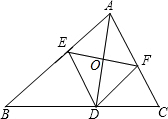 如图,在△ABC中,AD是△ABC的角平分线,DE∥AC,DF∥AB,EF交AD于点O,请问DO是△DEF的角平分线吗?请说明理由.
如图,在△ABC中,AD是△ABC的角平分线,DE∥AC,DF∥AB,EF交AD于点O,请问DO是△DEF的角平分线吗?请说明理由.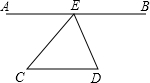 如图,已知点A,E,B在一同条直线上,设∠CED=x,∠C+∠D=y.
如图,已知点A,E,B在一同条直线上,设∠CED=x,∠C+∠D=y.