题目内容
5．解下列方程：（1）2x2+3x=3；
（2）x2-1=3x-3．
分析 （1）原式整理后，利用公式法分解即可；
（2）原式变形后，利用因式分解法求出解即可．
解答 解：（1）方程整理得：2x2+3x-3=0，
这里a=2，b=3，c=-3，
∵△=9+24=33，
∴x=$\frac{-3±\sqrt{33}}{4}$；
（2）方程整理得：（x+1）（x-1）-3（x-1）=0，即（x-1）（x+1-3）=0，
解得：x=1或x=2．
点评 此题考查了解一元二次方程-因式分解法，以及公式法，熟练掌握各种解法是解本题的关键．
练习册系列答案
相关题目
16．
如图，在△ABC中，∠B=85°，∠ACB=45°，若CD∥AB，则∠ACD的度数为（ ）
如图，在△ABC中，∠B=85°，∠ACB=45°，若CD∥AB，则∠ACD的度数为（ ）| A． | 40° | B． | 45° | C． | 50° | D． | 60° |
13．
如图，AB是⊙O的切线，B为切点，若∠ABC=120°，AB=2$\sqrt{3}$，AC经过点O，与⊙O分别相交于点D，C，则阴影部分的面积是（ ）
如图，AB是⊙O的切线，B为切点，若∠ABC=120°，AB=2$\sqrt{3}$，AC经过点O，与⊙O分别相交于点D，C，则阴影部分的面积是（ ）| A． | 2$\sqrt{3}$ | B． | $\frac{π}{6}$ | C． | 4$\sqrt{3}$-$\frac{2π}{3}$ | D． | 2$\sqrt{3}$-$\frac{2π}{3}$ |
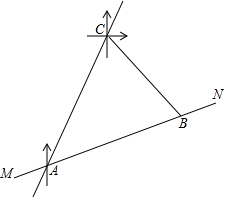超速行驶是一种十分危险的违法驾驶行为，在一条笔直的高速公路MN上，小型车限速为每小时120千米，设置在公路旁的超速监测点C，现测得一辆小型车在监测点C的南偏西30°方向的A处，7秒后，测得其在监测点C的南偏东45°方向的B处，已知BC=200米，B在A的北偏东75°方向，请问：这辆车超速了吗？通过计算说明理由．（参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）
如图，小明在A处测得风筝（C处）的仰角为30°，同时在A正对着风筝方向距A处30米的B处，小明测得风筝的仰角为60°，求风筝此时的高度．（结果保留根号）