题目内容
给出下列各式:
①(x+2y)2=x2+2xy+4y2;②(m2)3=m5;③5b4-4b3=b;④(-x-y)(x+y)=x2-y2,
其中运算错误的有( )
①(x+2y)2=x2+2xy+4y2;②(m2)3=m5;③5b4-4b3=b;④(-x-y)(x+y)=x2-y2,
其中运算错误的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:完全平方公式,合并同类项,幂的乘方与积的乘方,平方差公式
专题:
分析:根据完全平方公式,幂的乘方,合并同类项分别求出每个式子的值,再判断即可.
解答:解:(x+2y)2=x2+4xy+4y2,(m2)3=m5,5b4-4b3和b不相等,(-x-y)(x+y)=-(x+y)2=-x2-2xy-y2,∴①②③④都错误;
故选D.
故选D.
点评:本题考查了完全平方公式,幂的乘方,合并同类项的应用,主要考查学生的计算能力和判断能力.

练习册系列答案
相关题目
关于x的方程k2x2+(2k-1)x+1=0有实数根,则k的取值范围是( )
A、k≤
| ||
B、k≤
| ||
C、k<
| ||
D、k≥
|
9的平方根是( )
| A、3 | ||
| B、±3 | ||
| C、-3 | ||
D、±
|
下列说法正确的是( )
| A、数轴上的点与有理数一一对应 |
| B、数轴上的点与无理数一一对应 |
| C、数轴上的点与整数一一对应 |
| D、数轴上的点与实数一一对应 |
二元一次方程3x+y=7的正整数解有( )
| A、一个 | B、二个 | C、三个 | D、无数个 |
 如图,点D在直线AE上,量得∠CDE=∠A=∠C,有以下三个结论:
如图,点D在直线AE上,量得∠CDE=∠A=∠C,有以下三个结论:①AB∥CD;②AD∥BC;③∠B=∠CDA.
则正确的结论是( )
| A、①②③ | B、①② | C、① | D、②③ |
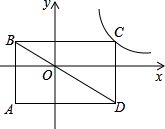 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C 在反比例函数y=
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C 在反比例函数y=