题目内容
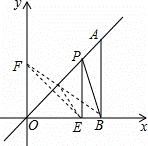
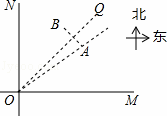
如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
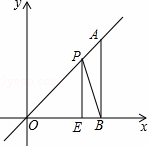
A. 4+2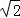 B. 4+
B. 4+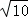 C. 6 D. 4
C. 6 D. 4
C
考点: 轴对称-最短路线问题;一次函数图象上点的坐标特征.
分析: 在y轴的正半轴上截取OF=OE=3,连接EF,证得F是E关于直线y=x的对称点,连接BF交OA于P,此时△BEP周长最小,最小值为BF+EB,根据勾股定理求得BF,因为BE=1,所以△BEP周长最小值为BF+EB=5+1=6.
解答: 解:在y轴的正半轴上截取OF=OE=3,连接EF,
∵A点为直线y=x上一点,
∴OA垂直平分EF,
∴E、F是直线y=x的对称点,
连接BF交OA于P,根据两点之间线段最短可知此时△BEP周长最小,最小值为BF+EB;
∵OF=3,OB=4,
∴BF=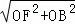 =5,
=5,
∵EB=4﹣3=1,
△BEP周长最小值为BF+EB=5+1=6.
故选C.
点评: 本题考查了轴对称的判定和性质,轴对称﹣最短路线问题,勾股定理的应用等,作出P点是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
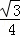 AG2.其中正确的结论( )
AG2.其中正确的结论( )
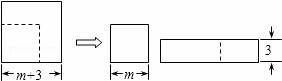

 ,求正方形ADCE周长.
,求正方形ADCE周长.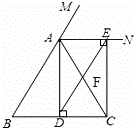
 的解集为 .
的解集为 .