题目内容
根据下面表格中的对应值:
x 3.24 3.25 3.26
ax2+bx+c ﹣0.02 0.01 0.03
判断关于x的方程ax2+bx+c=0(a≠0)的一个解x的范围是( )
A. x<3.24 B. 3.24<x<3.25 C. 3.25<x<3.26 D. x>3.26
B
考点: 估算一元二次方程的近似解.
分析: 根据表中数据得到x=3.24时,ax2+bx+c=﹣0.02;x=3.25时,ax2+bx+c=0.01,则x取2.24到2.25之间的某一个数时,使ax2+bx+c=0,于是可判断关于x的方程ax2+bx+c=0(a≠0)的一个解x的范围是3.24<x<3.25.
解答: 解:∵x=3.24时,ax2+bx+c=﹣0.02;x=3.25时,ax2+bx+c=0.01,
∴关于x的方程ax2+bx+c=0(a≠0)的一个解x的范围是3.24<x<3.25.
故选B.
点评: 本题考查了估算一元二次方程的近似解:用列举法估算一元二次方程的近似解,具体方法是:给出一些未知数的值,计算方程两边结果,当两边结果愈接近时,说明未知数的值愈接近方程的根.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
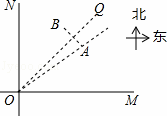

 .⊙P运动一圈与△OBC的边相切 次,每次相切时,点P到等边三角形顶点最近距离是 .
.⊙P运动一圈与△OBC的边相切 次,每次相切时,点P到等边三角形顶点最近距离是 .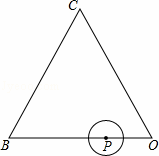
 ,求正方形ADCE周长.
,求正方形ADCE周长.