题目内容
已知关于x的方程(k-2)2x2+(2k+1)x+1=0有实数根,求k的取值范围.
考点:根的判别式,一元一次方程的解
专题:计算题
分析:分类讨论:当k-2=0,解k=2,原方程为一元一次方程,有一个实数根;当k-2≠0,即k≠2,当△=(2k+1)2-4(k-2)2≥0方程有实数根,然后综合两种情况得到k的取值范围.
解答:解:当k-2=0,解k=2,原方程变形为5x+1=0,解得x=-
;
当k-2≠0,即k≠2,△=(2k+1)2-4(k-2)2≥0,解得k≥
,则k≥
且k≠2时,原方程有两个实数根,
所以k≥
时,原方程有实数根.
| 1 |
| 5 |
当k-2≠0,即k≠2,△=(2k+1)2-4(k-2)2≥0,解得k≥
| 3 |
| 4 |
| 3 |
| 4 |
所以k≥
| 3 |
| 4 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.

练习册系列答案
相关题目
下列语句是命题的是( )
| A、相等的角是对顶角 |
| B、同位角相等吗? |
| C、国庆60周年大阅兵好壮观呀! |
| D、过一点作已知直线的垂线 |
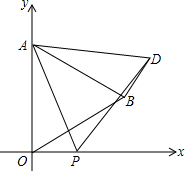 在平面直角坐标系中,已知点O为坐标原点,点A(0,4).在y轴右侧作等边△AOB,点B在第一象限.点P是x轴上的一个动点,连接AP,在右侧作等边△ADP,当四边形AODB是梯形时,求点P的坐标.
在平面直角坐标系中,已知点O为坐标原点,点A(0,4).在y轴右侧作等边△AOB,点B在第一象限.点P是x轴上的一个动点,连接AP,在右侧作等边△ADP,当四边形AODB是梯形时,求点P的坐标. 如图,AC=DB,∠ACB=∠DBC.找出图中所有的全等三角形,并说明理由.
如图,AC=DB,∠ACB=∠DBC.找出图中所有的全等三角形,并说明理由.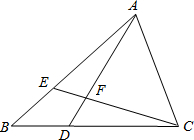 如图所示,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于F,试判断AF和CF的数量关系,并说明理由.
如图所示,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于F,试判断AF和CF的数量关系,并说明理由.