题目内容
5.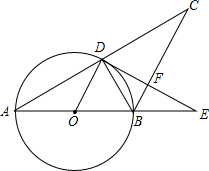 如图,在△ABC中,AB=BC,以AB为直径的圆O交BC于点D,过点D作DF⊥BC,交AB的延长线于E,垂足为F.若∠A=30°,BC=6,则DF=$\frac{3\sqrt{3}}{2}$.
如图,在△ABC中,AB=BC,以AB为直径的圆O交BC于点D,过点D作DF⊥BC,交AB的延长线于E,垂足为F.若∠A=30°,BC=6,则DF=$\frac{3\sqrt{3}}{2}$.
分析 由AB为直径,根据圆周角定理,可求得∠ADB=90°,即可得∠BDC=90°,然后由AB=BC,∠A=30°,BC=6,求得BD的长,继而求得答案.
解答 解:∵AB为直径,
∴∠ADB=90°,
∴∠BDC=90°,
∵AB=BC,
∴∠C=∠A=30°,
∴BD=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3,∠CBD=90°-∠C=60°,
∵DF⊥BC,
∴DF=BD•sin60°=3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$.
故答案为:$\frac{3\sqrt{3}}{2}$.
点评 此题考查了圆周角定理以及解直角三角形的知识.注意灵活应用直角三角形的性质是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.在△ABC和△A′B′C′中,∠B=∠B′,下列条件不能判断这两个三角形相似的是( )
| A. | ∠A=∠C′ | B. | ∠A=∠A′ | C. | $\frac{AB}{BC}=\frac{A′B′}{B′C′}$ | D. | $\frac{AB}{AC}=\frac{A′B′}{A′C′}$ |
10.在祁家河初中组织的演讲比赛中,七、八年级各有两名同学进入决赛,九年级有一名同学进入决赛,那么九年级同学获得第一名或第二名的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
14.为了建设绿色校园,学校去年年底的绿化面积为2000平方米,预计到明年年底增加到4200平方米,求这两年绿化面积的年平均增长率.下面所列方程正确的是( )
| A. | 2000(1-a%)2=4200 | B. | 2000(1+a%)2=4200 | C. | 2000(1-2a%)=4200 | D. | 2000(1-a2%)2=4200 |
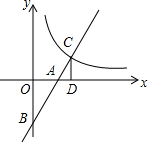 如图,直线y=kx-2(k>0)与双曲线$y=\frac{k}{x}$在第一象限内的交点为C,与x轴,y轴的交点分别为A,B,过点C作CD⊥x轴,垂足为D.若△OAB与△ACD的面积比为4:1,则k的值等于$\sqrt{3}$.
如图,直线y=kx-2(k>0)与双曲线$y=\frac{k}{x}$在第一象限内的交点为C,与x轴,y轴的交点分别为A,B,过点C作CD⊥x轴,垂足为D.若△OAB与△ACD的面积比为4:1,则k的值等于$\sqrt{3}$.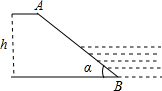 如图所示,一水库迎水坡AB的坡度i=1:2,则求坡角α的正弦值sinα=$\frac{\sqrt{5}}{5}$.
如图所示,一水库迎水坡AB的坡度i=1:2,则求坡角α的正弦值sinα=$\frac{\sqrt{5}}{5}$.