题目内容
 如图,在△ACB中,∠ACB=90°,∠B=60°,作边AC的垂直平分线l交AB于点D,过点C作AB的平行线交l于点E,判断四边形DBCE的形状,并说明理由.
如图,在△ACB中,∠ACB=90°,∠B=60°,作边AC的垂直平分线l交AB于点D,过点C作AB的平行线交l于点E,判断四边形DBCE的形状,并说明理由.考点:菱形的判定,线段垂直平分线的性质
专题:
分析:首先证得四边形DBCE为平行四边形,然后证得CB=DB,利用邻边相等的平行四边形是菱形判定该四边形是菱形即可.
解答: 答:四边形DBCE为菱形.
答:四边形DBCE为菱形.
证明:连接CD,
∵l垂直平分AC,
∴AD=DC,∠EOC=90°,
∵∠EOC=∠ACB,
∴ED∥BC,
又∵CE∥AB,
∴四边形DBCE为平行四边形.
∵AD=DC,
∴∠A=∠ACD,
∴∠DCB=90°-∠ACD=90°-∠A=∠B,
∴CD=DB,
∵∠B=60°,
∴△CDB为等边三角形,
∴CB=DB,
∴四边形DBCE为菱形.
 答:四边形DBCE为菱形.
答:四边形DBCE为菱形.证明:连接CD,
∵l垂直平分AC,
∴AD=DC,∠EOC=90°,
∵∠EOC=∠ACB,
∴ED∥BC,
又∵CE∥AB,
∴四边形DBCE为平行四边形.
∵AD=DC,
∴∠A=∠ACD,
∴∠DCB=90°-∠ACD=90°-∠A=∠B,
∴CD=DB,
∵∠B=60°,
∴△CDB为等边三角形,
∴CB=DB,
∴四边形DBCE为菱形.
点评:本题考查了菱形的判定,牢记菱形的判定定理是解答本题的关键,难度不大.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
小方家距学校为1km,小强家距离学校为2km,则小方家与小强家的距离为( )
| A、1km | B、2km |
| C、3km | D、不能确定 |
 如图,已知点B、D、E、C在同一直线上,∠ADE=∠AED,BD=CE.
如图,已知点B、D、E、C在同一直线上,∠ADE=∠AED,BD=CE.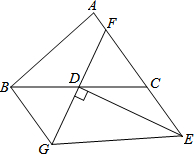 如图,在△ABC中,已知D是BC边的中点,过点D的直线GF交AC于F,交AC的平行线BG于点G,DE⊥GF,交AC的延长线于点E,联结EG.
如图,在△ABC中,已知D是BC边的中点,过点D的直线GF交AC于F,交AC的平行线BG于点G,DE⊥GF,交AC的延长线于点E,联结EG. 美化城市,改善人们的居住环境已成为城市建设的一项重要内容.某市区近几年来,通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加
美化城市,改善人们的居住环境已成为城市建设的一项重要内容.某市区近几年来,通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加