Question

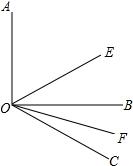如图所示，已知∠AOB=90°，∠BOC=30°，OE平分∠AOB，OE平分∠AOB，OF平分∠BOC．
（1）求∠EOF的度数；
（2）使条件中的∠AOB=110°，∠BOC=130°，求∠EOF的度数；
（3）使条件中的∠AOB=α，∠BOC=β，求∠EOF的度数．

Answer 1

考点：角的计算,角平分线的定义

专题：

分析：（1）∠AOB=90°，∠BOC=30°，OE平分∠AOB，OF平分∠BOC，可得到∠BOE和∠BOF的度数，∠EOF=∠BOE+∠BOF，即得；
（2）根据角平分线的定义，可得∠BOE和∠BOF的度数，∠BOE+∠BOF=∠EOF，即得；
（3）同（2），分别得出∠BOE和∠BOF的度数，即可求得代入∠EOF．

解答：解：∵OE平分∠AOB，OF平分∠BOC，
∴∠EOB=

1

2

∠AOB，∠BOF=

1

2

∠BOC，
∴∠EOF=∠EOB+∠BOF=

1

2

（∠AOB+∠BOC）．即∠EOF=

1

2

（∠AOB+∠BOC）．
（1）当∠AOB=90°，∠BOC=30°时，
∠EOF=

1

2

（∠AOB+∠BOC）=

1

2

×（90°+30°）=60°．


（2）当∠AOB=110°，∠BOC=130°时，
∠EOF=

1

2

（∠AOB+∠BOC）=

1

2

×（110°+130°）=120°．

（3）当∠AOB=α，∠BOC=β时，
∠EOF=

1

2

（∠AOB+∠BOC）=

1

2

×（α+β）．

点评：本题利用角平分线定理来作为一个例子，逐步引导学生从一般的问题中总结规律，发现隐藏的题后的结论，鼓励学生在以后的学习中要善于和总结规律和结论．