题目内容

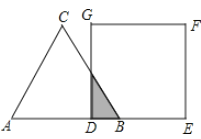
【题目】如图，等边的边AB与正方形DEFG的边长均为2，且AB与DE在同一条直线上，开始时点B与点D重合，让沿这条直线向右平移，直到点B与点E重合为止，设BD的长为x，与正方形DEFG重叠部分（图中阴影部分）的面积为y，则y与x之间的函数关系的图象大致是（ ）

A.B.C.D.

【答案】D

【解析】

此题可分为两段求解，即B从D点运动到DE的中点和A从DE的中点运动到E点，列出面积随动点变化的函数关系式即可．

解：设BD的长为x，△ABC与正方形DEFG重合部分（图中阴影部分）的面积为y，

当B从D点运动到DE的中点时，即0≤x≤1时，y=×x×x=x2．

当B从DE中点运动到E点时，即1＜x≤2时，y=-（2-x）×（2-x）=-x2+2x-

由函数关系式可看出D中的函数图象与所求的分段函数对应．

故选D．

练习册系列答案
相关题目

【题目】如图，AB是⊙O的切线，切点为B，OA交⊙O于点C，且AC=OC.

（1）求弧BC的度数；

（2）设⊙O的半径为5，求图中阴影部分的面积．

【题目】同学发现在宾馆房间的洗手盘台面上有一瓶洗手液（如图①）．于是好奇的小王同学进行了实地测量研究．当小王用一定的力按住顶部A下压如图②位置时，洗手液从喷口B流出，路线近似呈抛物线状，且a＝﹣．洗手液瓶子的截面图下部分是矩形CGHD．小王同学测得：洗手液瓶子的底面直径GH＝12cm，喷嘴位置点B距台面的距离为16cm，且B、D、H三点共线．小王在距离台面15.5cm处接洗手液时，手心Q到直线DH的水平距离为3cm，若学校组织学生去南京进行研学实践活动，若小王不去接，则洗手液落在台面的位置距DH的水平距离是（　　）cm．

A.12B.12C.6D.6

【题目】如图，矩形窗户边框ABCD由矩形AEFD，矩形BNME，矩形CFMN组成，其中AE：BE=1：3.已知制作一个窗户边框的材料的总长是6米，设BC=x(米)，窗户边框ABCD的面积为S(米2)

(1)①用x的代数式表示AB；

②求x的取值范围.

(2)求当S达到最大时，AB的长.

【题目】对钝角α，定义三角函数值如下：

sinα＝sin(180°－α)，cosα＝－cos(180°－α)．

(1)求sin120°，cos120°的值；

(2)若一个钝角三角形的三个内角比是1：1：4，点A，B是这个三角形的两个顶点，sinA，cosB是方程4x2－mx－1＝0的两个不相等的实数根，求m的值及∠A和∠B的度数．

【题目】已知抛物线与轴的交点分别为（1，0）、（3，0），与轴的交点为．

（1）求抛物线的解析式和顶点坐标；

（2）点（4，）和（，）为抛物线上的两点，当时，写出的取值范围；

（3）在抛物线的对称轴上是否存在点,使最大?若存在,请求出点的坐标;若不存在，请说明理由

【题目】将一副三角板与（其中，，）如图摆放，中所对的直角边与的斜边恰好重合。以为直径的圆经过点C，且与相交于点E，连接，连接并延长交于F.

（1）求证：平分；

（2）求与的面积的比值.

【题目】有一组邻边相等的凸四边形叫做“和睦四边形”，寓意是全世界和平共处，睦邻友好，共同发展.如菱形，正方形等都是“和睦四边形”.

（1）如图1，BD平分∠ABC，AD∥BC，求证:四边形ABCD为“和睦四边形”；

（2）如图2，直线与x轴、y轴分别交于A、B两点，点P、Q分别是线段OA、AB上的动点.点P从点A出发,以每秒4个单位长度的速度向点O运动.点Q从点A出发,以每秒5个单位长度的速度向点B运动.P、Q两点同时出发，设运动时间为t秒.当四边形BOPQ为“和睦四边形”时，求t的值；

（3）如图3，抛物线与轴交于A、B两点（点A在点B的左侧），与y轴交于点，抛物线的顶点为点D.当四边形COBD为“和睦四边形”，且CD=OC.抛物线还满足：①；②顶点D在以AB为直径的圆上. 点是抛物线上任意一点，且.若恒成立，求m的最小值.

【题目】如图，一艘海轮位于灯塔P的北偏东55方向，距离灯塔2海里的点A处，如果海轮沿正南方向航行到灯塔的正东方向，海轮航行的距离AB长是（ ）

A.2cos55o海里B.海里C.2sin55海里D.海里

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网