Question

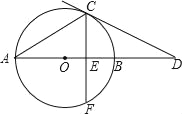
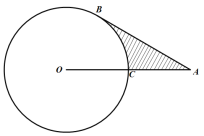
【题目】如图，AB是⊙O的切线，切点为B，OA交⊙O于点C，且AC=OC.

（1）求弧BC的度数；

（2）设⊙O的半径为5，求图中阴影部分的面积．

Answer 1

【答案】（1）60°；（2）.

【解析】

（1）连接OB、BC，根据切线的性质求得OB⊥AB，根据直角三角形斜边中线的性质得出BC=OA，进而求得OB=BC=OC，得出△OBC是等边三角形，求得∠BOC=60°，即可求得的度数；

（2）先求得直角三角形的面积和扇形的面积，根据S阴影=S△AOB﹣S扇形即可求得．

（1）连接OB、BC．

∵AB是圆O的切线，切点为B，∴OB⊥AB．

∵AC=OC，∴BC=OA．

∵AC=OC=OA，∴OB=BC=OC，∴△OBC是等边三角形，∴∠BOC=60°，∴的度数为60°；

（2）∵∠BOC=60°，OA=10，∴AB=sin60°OA=×10=5，∴S△AOB=ABOB=×5×5=．

∵S扇形=×60=，∴S阴影=S△AOB﹣S扇形=．