题目内容
1.在反比例函数y=$\frac{-k-4}{x}$图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是k<-4.分析 根据反比例函数的性质可得-k-4>0,再解即可.
解答 解:∵在反比例函数y=$\frac{-k-4}{x}$图象的每一支曲线上,y都随x的增大而减小,
∴-k-4>0,
解得:k<-4,
故答案为:k<-4.
点评 此题主要考查了反比例函数的性质,关键是掌握(1)反比例函数y=$\frac{k}{x}$(k≠0)的图象是双曲线;
(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;
(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
11.下列说法正确的是( )
| A. | 全等三角形是指形状相同的两个三角形 | |
| B. | 全等三角形是指面积相等的两个三角形 | |
| C. | 周长和面积都相等的两个三角形全等 | |
| D. | 有两组角和一组边分别相等的两个三角形全等 |
6.大于-1而小于$\sqrt{15}$的整数是( )
| A. | 0、1、2、3 | B. | 1、2、3 | C. | 2、3、4 | D. | 0、1、2、3、4 |
3.下列各组线段中,成比例线段的组是( )
| A. | 3cm,4cm,5cm,8cm | B. | 1cm,3cm,4cm,8cm | ||
| C. | 2.1cm,3.2cm,5.4cm,6.5cm | D. | 0.15cm,0.18cm,4cm,4.8cm. |
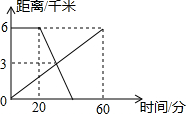 已知A、B两地相距4千米,上午8:00,甲从A地出发步行到B地,8:20乙从B地出发骑自行车到A地,甲乙两人离A地的距离y(千米)与甲所用的时间X(分)之间的关系如图所示,由图中的信息可知:
已知A、B两地相距4千米,上午8:00,甲从A地出发步行到B地,8:20乙从B地出发骑自行车到A地,甲乙两人离A地的距离y(千米)与甲所用的时间X(分)之间的关系如图所示,由图中的信息可知: