题目内容
4．一艘船从甲码头到乙码头顺流而行，用了2h；从乙码头返回甲码头逆流而行，用了2.5h．已知水流的速度是3km/h，则船在静水中的平均速度为（ ）| A． | 27 km/h | B． | 25 km/h | C． | 6.75 km/h | D． | 3 km/h |
分析 等量关系为：顺水速度×顺水时间=逆水速度×逆水时间．即：2×（静水速度+水流速度）=2.5×（静水速度-水流速度）．
解答 解：设船在静水中的平均速度为xkm/h，
根据往返路程相等，列得2（x+3）=2.5（x-3），
去括号，得2x+6=2.5x-7.5，
移项、合并同类项，得0.5x=13.5，
系数化为1，得x=27．
答：船在静水中的平均速度为27km/h．
故选A．
点评 本题考查了一元一次方程的应用，难度不大，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
15．下列方程是一元二次方程的是（ ）
| A． | 3x2-7=5y+1 | B． | $\frac{\sqrt{5}}{3}$x-$\sqrt{3}$=$\frac{1}{2}$x2+x | ||
| C． | 2x2-7y-2=0 | D． | 3x2-5x+7=3x2+6x-4 |
19．
如图，一条公路的转弯处是一段圆弧（图中的$\widehat{AB}$），点O是这段弧的圆心，C是$\widehat{AB}$上一点，OC⊥AB，垂足为D，AB=160m，CD=40m，则这段弯路的半径是（ ）
如图，一条公路的转弯处是一段圆弧（图中的$\widehat{AB}$），点O是这段弧的圆心，C是$\widehat{AB}$上一点，OC⊥AB，垂足为D，AB=160m，CD=40m，则这段弯路的半径是（ ）| A． | 60m | B． | 80m | C． | 100m | D． | 120m |
16．下列运算结果正确的是（ ）
| A． | x3•x3=2x3 | B． | （-x3）2=-x6 | C． | （5x）3=125x3 | D． | x5÷x=x5 |
13．二次根式$\sqrt{x+7}$有意义，则x的取值范围是（ ）
| A． | x≤-7 | B． | x≥-7 | C． | x＜-7 | D． | x＞-7 |
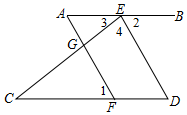完成下面的推理填空