题目内容
1.解答下列各题:(1)解方程:x2-4x-3=0;
(2)计算:$({\sqrt{48}+\frac{1}{4}\sqrt{6}})÷\sqrt{27}$.
分析 (1)利用配方法得到(x-2)2=7,然后利用直接开平方法解方程;
(2)先把各二次根式化为最简二次根式,然后进行二次根式的乘法运算.
解答 解:(1)x2-4x=3,
x2-4x+4=7,
(x-2)2=7,
x-2=±$\sqrt{7}$,
所以x1=2+$\sqrt{7}$,x2=2-$\sqrt{7}$;
(2)原式=(4$\sqrt{3}$+$\frac{\sqrt{6}}{4}$)÷3$\sqrt{3}$
=$\frac{4}{3}$+$\frac{\sqrt{2}}{12}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
9.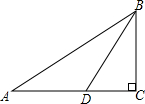 如图,在Rt△ABC中,∠C=90°,BD是角平分线,若CD=m,AB=n,则△ABD的面积是( )
如图,在Rt△ABC中,∠C=90°,BD是角平分线,若CD=m,AB=n,则△ABD的面积是( )
 如图,在Rt△ABC中,∠C=90°,BD是角平分线,若CD=m,AB=n,则△ABD的面积是( )
如图,在Rt△ABC中,∠C=90°,BD是角平分线,若CD=m,AB=n,则△ABD的面积是( )| A. | mn | B. | $\frac{1}{2}mn$ | C. | 2mn | D. | $\frac{1}{3}mn$ |
10.已知对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,则它的对称轴为( )
| A. | x=1 | B. | x=2 | C. | x=3 | D. | x=2.5 |
 如图,同一数轴上四点A,B,C,D所对应的数分别为a,b,c,d,且要邻两刻度的距离表示单位长度,若3a-2b=0,则数轴上点c对应的数为2,a+b-c-d=5.
如图,同一数轴上四点A,B,C,D所对应的数分别为a,b,c,d,且要邻两刻度的距离表示单位长度,若3a-2b=0,则数轴上点c对应的数为2,a+b-c-d=5.