题目内容
11．
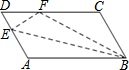如图，平行四边形ABCD中，点E在边AD上，以BE为折痕，将△ABE折叠，使点A恰好落在CD上的点F，若△BCF的周长为14，CF的长为3，则△DEF的周长为（ ）| A． | 8 | B． | 7 | C． | 6 | D． | 5 |
分析 由折叠的性质得出BF=AB，EF=AE，由△BCF的周长得出BC+DC=11，即可求出△DEF的周长．
解答 解：由折叠的性质得：△FBE≌△ABE，
∴BF=AB，EF=AE，
∵四边形ABCD是平行四边形，
∴AB=DC，AD=BC，
∵△BCF的周长为14，
∴BC+BF+CF=14，
∴BC+DC=14-3=11，
∴△DEF的周长=DE+EF+DF=DE+AE+DC-CF=AD+DC-CF=11-3=8；
故选：A．
点评 本题考查了翻折变换的性质、平行四边形的性质、三角形周长的计算；熟练掌握翻折变换和平行四边形的性质，并能进行推理计算是解决问题的关键．
练习册系列答案
相关题目
6．一个图形无论经过平移还是旋转，有以下说法：
（1）对应线段平行；
（2）对应线段相等；
（3）对应角相等；
（4）不改变图形的形状和大小，
其中正确的有（ ）
（1）对应线段平行；
（2）对应线段相等；
（3）对应角相等；
（4）不改变图形的形状和大小，
其中正确的有（ ）
| A． | （1）（2）（3） | B． | （1）（2）（4） | C． | （1）（3）（4） | D． | （2）（ 3）（4） |
7．
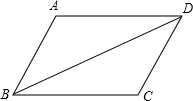在平行四边形ABCD中，∠BAD=110°，∠ABD=30°，则∠CBD度数为（ ）
在平行四边形ABCD中，∠BAD=110°，∠ABD=30°，则∠CBD度数为（ ）| A． | 30° | B． | 40° | C． | 70° | D． | 50° |
4．某公交公司有A，B型两种客车，它们的载客量和租金如下表：
红星中学根据实际情况，计划租用A，B型客车共5辆，同时送七年级师生到基地校参加社会实践活动，设租用A型客车x辆，根据要求回答下列问题：
（1）用含x的式子填写下表：
（2）若要保证租车费用不超过1900元，求x的最大值；
（3）在（2）的条件下，若七年级师生共有195人，写出所有可能的租车方案，并确定最省钱的租车方案．
| A | B | |
| 载客量（人/辆） | 45 | 30 |
| 租金（元/辆） | 400 | 280 |
（1）用含x的式子填写下表：
| 车辆数（辆） | 载客量 | 租金（元） | |
| A | x | 45x | 400x |
| B | 5-x | 30（5-x） | 280（5-x） |
（3）在（2）的条件下，若七年级师生共有195人，写出所有可能的租车方案，并确定最省钱的租车方案．
如图，在矩形ABCD中，点E是边CD的中点，将△ADE沿AE折叠后得到△AFE，且点F在矩形ABCD内部．将AF延长交边BC于点G．若CG：GB=1：k，求AD：AB（用含k的代数式表示）．
3．教练对小明推铅球的录像进行技术分析，发现铅球行进高度y（m）与水平距离x（m）间的关系为y=-$\frac{1}{12}$（x-4）2+3，由此可知铅球推出的距离是（ ）
| A． | 2m | B． | 8m | C． | 10m | D． | 12m |
20．已知x=-1是方程2x2+ax-5=0的一个根，则a的值是（ ）
| A． | -3 | B． | -4 | C． | 3 | D． | 7 |
1．在平面直角坐标系内，将直线y=-3x向下平移6个单位，得到直线所对应的解析式是（ ）
| A． | y=-3x+6 | B． | y=-3x-6 | C． | y=-4x | D． | y=-2x |