题目内容
1.某车间有20名工人,每人每天可以加工甲种零件5个或乙种零件4个,在这20名工人中,派x名工人加工甲种零件,其余人加工乙种零件.己知每加工一个甲种零件可获利16元,每加工一个乙种零件可获利24元.(1)写出此工厂每天所获利润y(元)与x(人)之间的函数关系式;
(2)若派10名工人加工甲种零件,求每天所获利润y;
(3)若要使车间每天获利1840元,则需要派多少名工人加工乙种零件?
分析 (1)根据题意可以得到y与x之间的函数关系式;
(2)将x=10代入第一问中求得的函数关系式,即可得到每天所获利润;
(3)将y=1840代入第一问中求得的函数关系式,即可求得x的值,然后用20-x求得需要派多少名工人加工乙种零件.
解答 解:(1)根据题意可得,
y=5x×16+(20-x)×4×24=80x+20×96-96x=-16x+1920.
即此工厂每天所获利润y(元)与x(人)之间的函数关系式是:y=-16x+1920.
(2)将x=10代入y=-16x+1920得,y=-16×10+1920=1760(元).
答:若派10名工人加工甲种零件,每天所获利润是1760元.
(3)将y=1840代入y=-16x+1920,得
1840=-16x+1920,
解得x=5.
20-5=15(人).
答:要使车间每天获利1840元,则需要派15名工人加工乙种零件.
点评 本题考查一次函数的应用,解题的关键是列出相应的函数关系式,注意第三问求得的x值是派往加工甲种零件的,还有用20-x才能得到派往加工乙种零件的工人数.

练习册系列答案
相关题目
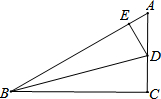 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,BD是△ABC角平分线,求tan15°的值.(提示:过点D作DE⊥AB.垂足为点E.)
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,BD是△ABC角平分线,求tan15°的值.(提示:过点D作DE⊥AB.垂足为点E.) 如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=80°,则∠B′OG的度数为50°.
如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=80°,则∠B′OG的度数为50°.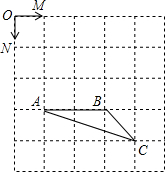 如图,已知正方形网格中每个小正方形的边长为1,点O、M、N、A、B、C都是小正方形的顶点.
如图,已知正方形网格中每个小正方形的边长为1,点O、M、N、A、B、C都是小正方形的顶点. 已知:点I是△ABC的内心,AI的延长线交外接圆于D.则DB与DI相等吗?为什么?
已知:点I是△ABC的内心,AI的延长线交外接圆于D.则DB与DI相等吗?为什么? 如图所示是由几个小立方块所搭的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,请画出相应几何体的主视图和左视图.
如图所示是由几个小立方块所搭的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,请画出相应几何体的主视图和左视图.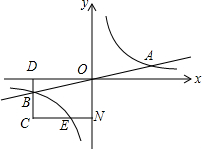 已知双曲线y=$\frac{k}{x}$与直线y=$\frac{1}{4}$x相交于A、B两点.过点B作矩形DCNO交x轴于点D.交Y轴于点N.交双曲线y=$\frac{k}{x}$于点E.若B是CD的中点,四边形OBCE的面积为4,则双曲线y=$\frac{k}{x}$的解析式为$\frac{4}{x}$.
已知双曲线y=$\frac{k}{x}$与直线y=$\frac{1}{4}$x相交于A、B两点.过点B作矩形DCNO交x轴于点D.交Y轴于点N.交双曲线y=$\frac{k}{x}$于点E.若B是CD的中点,四边形OBCE的面积为4,则双曲线y=$\frac{k}{x}$的解析式为$\frac{4}{x}$.