��Ŀ����
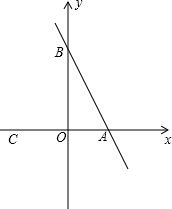 ��֪��ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA��3��0����B��O��4������C������ΪC��-2��O������P��ֱ��AB�ϵ�һ���㣬ֱ��CP��y�ύ�ڵ�D��
��֪��ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA��3��0����B��O��4������C������ΪC��-2��O������P��ֱ��AB�ϵ�һ���㣬ֱ��CP��y�ύ�ڵ�D����1����CP��ABʱ����OD�ij���
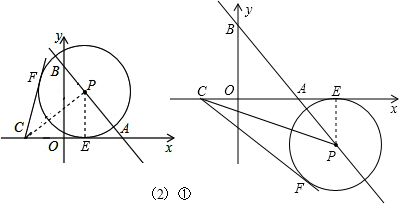
��2������P��ֱ��AB�ƶ�ʱ���Ե�PΪԲ�ģ���ABΪֱ������P������C����P���������ߣ��е�ֱ�Ϊ��E��F��
������P��x��������CE�ij���
�ڵ���P��ֱ��AB�ƶ�ʱ����̽���Ƿ�����ı���CEPF����С���S�������ڣ������S��ֵ���������ڣ���˵�����ɣ�
���㣺Բ���ۺ���
ר�⣺
��������1�����ݵ�A��B��C���������AB��OA��OB�ij��ȣ��ٸ���ȫ�������ε��ж������ʵó�OD�ij���
��2���������ֱ��AB�Ľ���ʽ��Ȼ�������P�����꣬�������ߵĶ���ɵõ�P��������ij��ȵ��ڡ�P�İ뾶��Ȼ�����õ�x��ֵ�����ɵý⣻
�ڸ��ݵ�P�����꣬���������ľ��빫ʽ���PC�ij��ȣ������ù��ɶ�����ʾ��CE��Ȼ��������߳������ɵ��ı���CEPF��������ڡ�PCE�������2����Ȼ����������ε������ʽ��ʽ���������ٸ��ݶ��κ�������ֵ������
��2���������ֱ��AB�Ľ���ʽ��Ȼ�������P�����꣬�������ߵĶ���ɵõ�P��������ij��ȵ��ڡ�P�İ뾶��Ȼ�����õ�x��ֵ�����ɵý⣻
�ڸ��ݵ�P�����꣬���������ľ��빫ʽ���PC�ij��ȣ������ù��ɶ�����ʾ��CE��Ȼ��������߳������ɵ��ı���CEPF��������ڡ�PCE�������2����Ȼ����������ε������ʽ��ʽ���������ٸ��ݶ��κ�������ֵ������
����⣺��1����ͼ1���ߵ�A��B������ֱ�ΪA��3��0����B��O��4����
��AB=5��
�ߵ�C������ΪC��-2��O����
��AC=5��
��AB=5=AC��
�ڡ�AOB�͡�APC�У�
��
���AOB�ա�APC��AAS����
��AP=OA=3��CP=OB=4��
��BP=OC=2��
�ڡ�BDP�͡�CDO��
��
���BDP�ա�CDO��AAS����
��DP=OD��
��DP=OD=x����CD=4-x��
��x2+22=��4-x��2��
��ã�x=
����OD=
��
��2������ͼ��2���٣���AB����ʽΪy=ax+b����A��3��0����B��O��4��������ó���
��
��ã�
��
��AB�Ľ���ʽΪy=-
x+4��
���P��������x��-
x+4����
�ߡ�P��x�����У�
��|-
x+4|=
=
��
��-
x+4=
��-
x+4=-
��
���x=
��x=
��
���ԣ�CE=
-��-2��=
+2=
��
��CE=
-��-2��=
+2=
��
����ͼ��2����
�ߵ�P��x��-
x+4����C��-2��0����
��PC=
��
�ߡ�P�İ뾶Ϊ
=
��
����ݹ��ɶ����ã�CE=
=
=
��
�������߳���������PCE���PCF����ֱ��PC����Գƣ�
���ı���CEPF�����=2S��PCE=2��
•
��
=
��
��
x-2=0����x=
ʱ���ı���CEPF���������Сֵ����СֵΪ
��
=
��
��AB=5��
�ߵ�C������ΪC��-2��O����

��AC=5��
��AB=5=AC��
�ڡ�AOB�͡�APC�У�
|
���AOB�ա�APC��AAS����
��AP=OA=3��CP=OB=4��
��BP=OC=2��
�ڡ�BDP�͡�CDO��
|
���BDP�ա�CDO��AAS����
��DP=OD��
��DP=OD=x����CD=4-x��
��x2+22=��4-x��2��
��ã�x=
| 3 |
| 2 |
| 3 |
| 2 |
��2������ͼ��2���٣���AB����ʽΪy=ax+b����A��3��0����B��O��4��������ó���
|
��ã�
|

��AB�Ľ���ʽΪy=-
| 4 |
| 3 |
���P��������x��-
| 4 |
| 3 |
�ߡ�P��x�����У�
��|-
| 4 |
| 3 |
| AB |
| 2 |
| 5 |
| 2 |
��-
| 4 |
| 3 |
| 5 |
| 2 |
| 4 |
| 3 |
| 5 |
| 2 |
���x=
| 9 |
| 8 |
| 39 |
| 8 |
���ԣ�CE=
| 9 |
| 8 |
| 9 |
| 8 |
| 25 |
| 8 |
��CE=
| 39 |
| 8 |
| 39 |
| 8 |
| 55 |
| 8 |

����ͼ��2����
�ߵ�P��x��-
| 4 |
| 3 |
��PC=
(x+2)2+(-
|
�ߡ�P�İ뾶Ϊ
| AB |
| 2 |
| 5 |
| 2 |
����ݹ��ɶ����ã�CE=
| PC2-PE2 |
(x+2)2+(-
|
(
|
�������߳���������PCE���PCF����ֱ��PC����Գƣ�
���ı���CEPF�����=2S��PCE=2��
| 1 |
| 2 |
(
|
| 5 |
| 2 |
| 5 |
| 2 |
(
|
��
| 5 |
| 3 |
| 6 |
| 5 |
| 5 |
| 2 |
|
5
| ||
| 4 |
���������⿼����һ�κ��������⣬��Ҫ�漰���������ε��ж������ʣ����ɶ�����Ӧ�ã����߳������Լ������ľ��빫ʽ�����κ�������ֵ���⣬����ֱ�߽���ʽ�����P�������ǽ���Ĺؼ��������������ϴȽϸ��ӣ�����ʱҪ��ϸ���森

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ��������y=-
��ͼ��������y=- ��ͼ��8��8�������������н���ֱ������ϵ���� ֪A��2��4����B��4��2����C�ǵ�һ�����ڵ�һ����㣬�ɵ�C���߶�AB���һ����ABΪ�ף�������Ϊ�������ĵ��������Σ�����ͼ�Σ�������������⣺
��ͼ��8��8�������������н���ֱ������ϵ���� ֪A��2��4����B��4��2����C�ǵ�һ�����ڵ�һ����㣬�ɵ�C���߶�AB���һ����ABΪ�ף�������Ϊ�������ĵ��������Σ�����ͼ�Σ�������������⣺ ��ͼ��M��N��������ABCD��AB��CD�������㣬����MN�����ı���BCNM��MN�۵���ʹ��B����AD���ϵ�E������C���ڵ�F��
��ͼ��M��N��������ABCD��AB��CD�������㣬����MN�����ı���BCNM��MN�۵���ʹ��B����AD���ϵ�E������C���ڵ�F�� ��ͼ����֪����E��AC�ϣ�AB��CD����B=��AEB����D=��CED����֤��BE��ED��
��ͼ����֪����E��AC�ϣ�AB��CD����B=��AEB����D=��CED����֤��BE��ED��