题目内容
 如图,已知:点E在AC上,AB∥CD,∠B=∠AEB,∠D=∠CED.求证:BE⊥ED.
如图,已知:点E在AC上,AB∥CD,∠B=∠AEB,∠D=∠CED.求证:BE⊥ED.考点:平行线的判定与性质
专题:证明题
分析:过点E作EF∥AB,则EF∥CD,根据平行线的性质可以证得∠1=∠AEB=
∠AEF,∠2=∠CED=
∠CEF,即可求得∠1与∠2的和,从而证得.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:过点E作EF∥AB.
解:过点E作EF∥AB.
∵AB∥CD,
∴EF∥CD.
∵EF∥AB,
∴∠1=∠B.
∵∠B=∠AEB,
∴∠1=∠AEB=
∠AEF.
同理∠2=∠CED=
∠CEF.
∵∠AEF+∠CEF=180°,
∴∠1+∠2=∠BED=90°,即BE⊥ED.
 解:过点E作EF∥AB.
解:过点E作EF∥AB.∵AB∥CD,
∴EF∥CD.
∵EF∥AB,
∴∠1=∠B.
∵∠B=∠AEB,
∴∠1=∠AEB=
| 1 |
| 2 |
同理∠2=∠CED=
| 1 |
| 2 |
∵∠AEF+∠CEF=180°,
∴∠1+∠2=∠BED=90°,即BE⊥ED.
点评:本题考查了平行线的性质:两直线平行,内错角相等,正确作出辅助线是关键.

练习册系列答案
相关题目

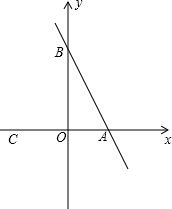 已知在平面直角坐标系中,点A、B的坐标分别为A(3,0)、B(O,4),点C的坐标为C(-2,O),点P是直线AB上的一动点,直线CP与y轴交于点D.
已知在平面直角坐标系中,点A、B的坐标分别为A(3,0)、B(O,4),点C的坐标为C(-2,O),点P是直线AB上的一动点,直线CP与y轴交于点D. 已知,如图,MN∥EH,AB∥CD,∠1=110°,求∠2的度数.
已知,如图,MN∥EH,AB∥CD,∠1=110°,求∠2的度数. 如图,已知AB=12米,MA⊥AB于A,MA=6米,射线BD⊥AB于B,P点从B向A运动,每秒走1米,Q点从B向D运动,每秒走2米,P、Q同时从B出发,则出发
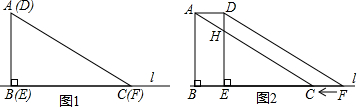
如图,已知AB=12米,MA⊥AB于A,MA=6米,射线BD⊥AB于B,P点从B向A运动,每秒走1米,Q点从B向D运动,每秒走2米,P、Q同时从B出发,则出发 如图,△ABC中,∠A=35°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=85°,则原三角形的∠ABC的度数为
如图,△ABC中,∠A=35°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=85°,则原三角形的∠ABC的度数为