��Ŀ����
4��̽������ͼ1����Rt��ABC�У���BAC=90�㣬��ABC=45�㣬����B��ֱ��MN��AC��DΪBC����һ�㣬����AD����DE��AD��MN�ڵ�E����DF��BC��AB�ڵ�F����֤��AD=DE��Ӧ�ã���ͼ2����Rt��ABC�У���BAC=90�㣬��ABC=30�㣬����B��ֱ��MN��AC��DΪBC����һ�㣬����AD����DE��AD��MN�ڵ�E����DF��BC��AB�ڵ�F��ֱ��д���߶�DE��AD��������ϵ������֤����
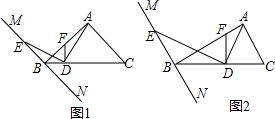
���� ��1������֤�á�BDE=��ADF���Լ���EBD=��AFD���ٵó���BDE�ա�FDA��ASA����������ɣ�
��2�����ȹ���D��DG��BC����AB�ڵ�G�������ó���EBD=��AGD��֤����BDE�ס�GDA���ɵó��𰸣�
��� ��1��֤������ͼ1�����С�BDE+��FDE=90�㣬
��DE��AD��
���FDE+��ADF=90�㣬
���BDE=��ADF��
�ߡ�BAC=90�㣬��ABC=45�㣬
���C=45�㣬
��MN��AC��
���EBD=180��-��C=135�㣬
�ߡ�BFD=45�㣬DF��BC��
���BFD=45�㣬BD=DF��
���AFD=135�㣬
���EBD=��AFD��
�ڡ�BDE�͡�FDA�У�
$\left\{\begin{array}{l}{��EBD=��AFD}\\{BD=DF}\\{��BDE=��ADF}\end{array}\right.$��
���BDE�ա�FDA��ASA����
��AD=DE��
��2���⣺DE=$\sqrt{3}$AD��
���ɣ���ͼ2�����С�BDE+��FDE=90�㣬
��DE��AD��
���FDE+��ADF=90�㣬
���BDE=��ADF��
�ߡ�BAC=90�㣬��ABC=30�㣬
���C=60�㣬
��MN��AC��
���EBD=180��-��C=120�㣬
�ߡ�ABC=30�㣬DF��BC��
���BFD=60�㣬
���AFD=120�㣬
���EBD=��AFD��
���BDE�ס�FDA
��$\frac{AD}{DE}$=$\frac{DF}{BD}$��
��Rt��BDF��
$\frac{DF}{BD}$=tan30��=$\frac{\sqrt{3}}{3}$��
��DE=$\sqrt{3}$AD��
���� ������Ҫ������ȫ�������ε��ж��������Լ����������ε��ж������ʣ��ó���EBD�ס�AFD�ǽ���ؼ���

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� ��ͼ����������A��B��C��D�ĸ��㣬���б�ʾ-3�ľ���ֵ�ĵ��ǣ�������
��ͼ����������A��B��C��D�ĸ��㣬���б�ʾ-3�ľ���ֵ�ĵ��ǣ�������| A�� | ��A | B�� | ��B | C�� | ��C | D�� | ��D |
| ͨ��ʱ��x/���� | 0��x��5 | 5��x��10 | 10��x��15 | 15��x��20 |
| Ƶ����ͨ�������� | 20 | 16 | 9 | 5 |
| A�� | 0.1 | B�� | 0.4 | C�� | 0.5 | D�� | 0.9 |
| A�� | 2 | B�� | 0 | C�� | -1 | D�� | -2 |
| A�� |  | B�� |  | C�� |  | D�� |  |
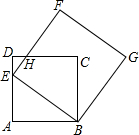 ��ͼ����EΪ������ABCD��AD���ϵ�һ�����㣬AB=16����BEΪ��������BEFG����EF���CD���ڵ�H��
��ͼ����EΪ������ABCD��AD���ϵ�һ�����㣬AB=16����BEΪ��������BEFG����EF���CD���ڵ�H��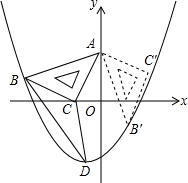 ��ͼ����ƽ��ֱ������ϵ�У���һ������Ϊ5�ĵ���ֱ�����ǰ�ABC���ڵڶ����ޣ���б�������������ϣ�ֱ�Ƕ���C������Ϊ��-1��0������B��������y=ax2+ax-2�ϣ�
��ͼ����ƽ��ֱ������ϵ�У���һ������Ϊ5�ĵ���ֱ�����ǰ�ABC���ڵڶ����ޣ���б�������������ϣ�ֱ�Ƕ���C������Ϊ��-1��0������B��������y=ax2+ax-2�ϣ� ��֪���κ���y=x2-��2k+1��x+k2+k��k��0��
��֪���κ���y=x2-��2k+1��x+k2+k��k��0��