题目内容
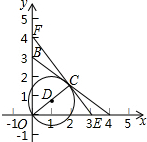 如图,在平面直角坐标系中,点A、B的坐标分别为(a,0),(0,b),且a:b=4:3,点C是AB的中点,以OC为直径作圆D,且圆D的直径为
如图,在平面直角坐标系中,点A、B的坐标分别为(a,0),(0,b),且a:b=4:3,点C是AB的中点,以OC为直径作圆D,且圆D的直径为| 5 |
| 2 |
(1)求A、B两点的坐标;
(2)过点C作圆D的切线EF,交x轴于E,交y轴于F,求EF的长;
(3)P是线段OA上的动点(不与O、A重合),设P的横坐标为x,那么当x分别取何值时,以OP为半径的圆P与直线AB相交、相切或相离?
考点:圆的综合题
专题:综合题
分析:(1)根据直角三角形斜边上的中线性质得到AB=2OC=5,设OA=4t,则OB=3t,利用勾股定理得到AB=5t,则5t=5,解得t=1,即可得到点坐标为(4,0),B点坐标为(0,3);
(2)⊙D交x轴于H,连接CH,如图1,先根据线段中点坐标公式得到C点坐标为(2,
),再根据圆周角定理由OC为直径得到∠OHC=90°,则OH=2,CH=
,
然后根据切线的性质得OC⊥EF,易证得Rt△OCH∽Rt△OEC,利用相似比可计算出OE=
,CE=
,再利用CH∥OF证明△ECH∽△EFO,于是可利用相似比可计算出EF;
(3)先讨论相切的条件:若⊙P与AB相切于G点时,连接PG,如图2,根据切线的性质得PG⊥AB,易证得Rt△APG∽Rt△ABO,利用相似比得到
=
,解得x=
,然后根据直线与圆的位置关系即可得到当0<x<
时,以OP为半径的圆P与直线AB相离;当x=
时,以OP为半径的圆P与直线AB相切;当
x≤4时,以OP为半径的圆P与直线AB相交.
(2)⊙D交x轴于H,连接CH,如图1,先根据线段中点坐标公式得到C点坐标为(2,
| 3 |
| 2 |
| 3 |
| 2 |
然后根据切线的性质得OC⊥EF,易证得Rt△OCH∽Rt△OEC,利用相似比可计算出OE=
| 25 |
| 8 |
| 15 |
| 8 |
(3)先讨论相切的条件:若⊙P与AB相切于G点时,连接PG,如图2,根据切线的性质得PG⊥AB,易证得Rt△APG∽Rt△ABO,利用相似比得到
| x |
| 3 |
| 4-x |
| 4 |
| 12 |
| 7 |
| 12 |
| 7 |
| 12 |
| 7 |
| 12 |
| 7 |
解答: 解:(1)在Rt△AOB中,∵点C是AB的中点,
解:(1)在Rt△AOB中,∵点C是AB的中点,
∴OC=
AB,
∴AB=2OC=2×
=5,
设OA=4t,则OB=3t,
∴AB=
=5t,
∴5t=5,解得t=1,
∴A点坐标为(4,0),B点坐标为(0,3);
(2)⊙D交x轴于H,连接CH,如图1,
∵点C是AB的中点,
∴C点坐标为(2,
),
∵OC为直径,
∴∠OHC=90°,即CH⊥x轴,
∴OH=2,CH=
,
∵EF为⊙D的切线,C为切点,
∴OC⊥EF,
∵∠COH=∠EOC,
∴Rt△OCH∽Rt△OEC,
∴OC:OE=OH:OC=CH:CE,
∴OE=
=
=
,CE=
=
=
,
∵CH∥OF,
∴△ECH∽△EFO,
∴
=
,即
=
,
∴EF=
;
(3)若⊙与AB相切于G点时,连接PG,如图2,P点坐标为(x,0)
∵与AB相切于G点,
∴PG⊥AB,
∵∠PAG=∠BAO,
∴Rt△APG∽Rt△ABO,
∴
=
,即
=
,
解得x=
,
∴当0<x<
时,以OP为半径的圆P与直线AB相离;当x=
时,以OP为半径的圆P与直线AB相切;当
x≤4时,以OP为半径的圆P与直线AB相交.
 解:(1)在Rt△AOB中,∵点C是AB的中点,
解:(1)在Rt△AOB中,∵点C是AB的中点,∴OC=
| 1 |
| 2 |
∴AB=2OC=2×
| 5 |
| 2 |
设OA=4t,则OB=3t,
∴AB=
| OA2+OB2 |
∴5t=5,解得t=1,
∴A点坐标为(4,0),B点坐标为(0,3);
(2)⊙D交x轴于H,连接CH,如图1,
∵点C是AB的中点,
∴C点坐标为(2,
| 3 |
| 2 |
∵OC为直径,
∴∠OHC=90°,即CH⊥x轴,
∴OH=2,CH=
| 3 |
| 2 |
∵EF为⊙D的切线,C为切点,
∴OC⊥EF,
∵∠COH=∠EOC,
∴Rt△OCH∽Rt△OEC,
∴OC:OE=OH:OC=CH:CE,
∴OE=
| OC2 |
| OH |
(
| ||
| 2 |
| 25 |
| 8 |
| OC•CH |
| OH |
| ||||
| 2 |
| 15 |
| 8 |
∵CH∥OF,
∴△ECH∽△EFO,

∴
| CE |
| EF |
| EH |
| EO |
| ||
| EF |
| ||
|
∴EF=
| 125 |
| 24 |
(3)若⊙与AB相切于G点时,连接PG,如图2,P点坐标为(x,0)
∵与AB相切于G点,
∴PG⊥AB,
∵∠PAG=∠BAO,
∴Rt△APG∽Rt△ABO,
∴
| PG |
| OB |
| AP |
| AO |
| x |
| 3 |
| 4-x |
| 4 |
解得x=
| 12 |
| 7 |
∴当0<x<
| 12 |
| 7 |
| 12 |
| 7 |
| 12 |
| 7 |
点评:本题考查了圆的综合题:熟练掌握圆周角定理、切线的性质和直线与圆的位置关系的判定方法;理解坐标与图形性质;会运用勾股定理和相似比进行几何计算.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 实数x在数轴上的位置如图所示,则化简
实数x在数轴上的位置如图所示,则化简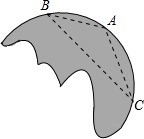 一天,小明不小心将手电筒上的圆形玻璃片打碎了,碎片中有一块如图所示,小明想去玻璃店重新配一块;
一天,小明不小心将手电筒上的圆形玻璃片打碎了,碎片中有一块如图所示,小明想去玻璃店重新配一块;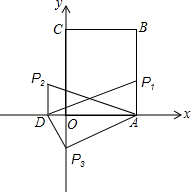 如图所示平面直角坐标系中,矩形OABC的顶点B的坐标为(4,8),若一次函数y=kx+2的图象平分矩形OABC的面积.
如图所示平面直角坐标系中,矩形OABC的顶点B的坐标为(4,8),若一次函数y=kx+2的图象平分矩形OABC的面积. 如图,已知点C在B点的北偏西60°的方向上,B点在A点的北偏东30°的方向上,试求∠ABC的度数.
如图,已知点C在B点的北偏西60°的方向上,B点在A点的北偏东30°的方向上,试求∠ABC的度数.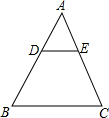 如图,△ABC中,已知,DE∥BC,AD=
如图,△ABC中,已知,DE∥BC,AD= 如图,在△ABC中,∠A=50°,BP平分∠ABC,CP平分∠ACB,则∠BPC的度数是
如图,在△ABC中,∠A=50°,BP平分∠ABC,CP平分∠ACB,则∠BPC的度数是