题目内容
 如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,若∠A=80°,则∠BOC=
如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,若∠A=80°,则∠BOC=考点:三角形内角和定理
专题:
分析:先根据三角形内角和定理求出∠ABC+∠ACB的度数,再由角平分线的性质得出∠OBC+∠OCB的度数,由三角形内角和定理即可得出结论.
解答:解:∵在△ABC中,∠A=80°,
∴∠ABC+∠ACB=180°-80°=100°,
∵∠ABC和∠ACB的平分线交于O点,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
×100°=50°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-50°=130°.
故答案为:130°.
∴∠ABC+∠ACB=180°-80°=100°,
∵∠ABC和∠ACB的平分线交于O点,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=180°-50°=130°.
故答案为:130°.
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 用圆心角为120°,半径为9cm的扇形纸片卷成一个圆锥形无底纸帽(如图),则这个纸帽的高是( )
用圆心角为120°,半径为9cm的扇形纸片卷成一个圆锥形无底纸帽(如图),则这个纸帽的高是( )A、
| ||
B、3
| ||
C、4
| ||
D、6
|
已知x=
+1,且x2=ax+b,则a,b的值分别为( )
| 5 |
| A、1,2 | B、2,2 |
| C、2,3 | D、2,4 |
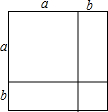 如图,这是某小区绿化带的平面示意图(单位m)
如图,这是某小区绿化带的平面示意图(单位m) 如图,在直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△ABO,点C为x轴正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.下列结论正确的有( )个:
如图,在直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△ABO,点C为x轴正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.下列结论正确的有( )个: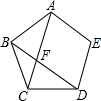 如图所示,正五边形ABCDE,连接对角线AC、BD,设AC与BD相交于点F.
如图所示,正五边形ABCDE,连接对角线AC、BD,设AC与BD相交于点F.