题目内容
6．
如图，以Rt△ABC的三边向外作正方形，若最大正方形的边长为13cm，以AC为边的正方形的面积为144，则AB长为5cm．
分析 由正方形的面积公式可知AC2，=144，BC2=132，SM=AB2，在Rt△ABC中，由勾股定理得AC2+AB2=BC2，由此可求SM．即可得出AB的长．
解答 解：∵在Rt△ABC中，由勾股定理得：AC2+AB2=BC2，
又∵AC2=144，BC2=169，SM=AB2，
∴SM=169-144=25，
∴AB=$\sqrt{25}$=5（cm）．
故答案为：5cm．
点评 本题考查了勾股定理及正方形面积公式的运用；解题关键是明确直角三角形的边长的平方即为相应的正方形的面积，难度一般．
练习册系列答案
相关题目
如图所示，线段AB=2.8m，点C分AB为AC和BC的比为2：$\frac{4}{5}$，D为AB中点，求CD的长．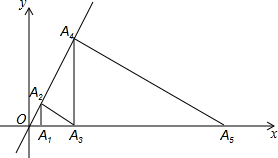
在直角坐标系中，点A1的坐标为（1，0），过点A1作x轴的垂线交直线y=2x于A2，过点A2作直线y=2x的垂线交x轴于A3，过点A3作x轴的垂线交直线y=2x于A4…，依此规律，则A2016的坐标为（51007，2×51007）．
如图，线段CD两个端点的坐标分别为C（3，3），D（4，1），以原点O为位似中心，在第一象限内将线段CD扩大为原来的两倍，得到线段AB，则线段AB的中点E的坐标为（7，4）．
如图，在△ABC中，AB=AC=2，∠B=75°，则点B到边AC的距离为1．