题目内容
20.(1)观察下列分解因式的过程:x2+2ax-3a2
=x2+2ax+a2-a2-3a2(先加上a2,再减去a2)
=(x+a)2-4a2(运用完全平方公式)
=(x+a+2a)(x+a-2a )(运用平方差公式)
=(x+3a)(x-a)
像上面那样通过加减项配出完全平方式后再把二次三项式分解因式的方法,叫做配方法.请你用配方法分解因式:m2-4mn+3n2
(2)先化简,再求值:$\frac{x}{x-y}$+$\frac{{y}^{2}}{x(x-y)^{2}}$÷$\frac{xy+{y}^{2}}{{y}^{2}-{x}^{2}}$,其中x=1,y=3.
分析 (1)原式利用阅读材料中的方法分解即可;
(2)原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的加法法则计算得到最简结果,把x与y的值代入计算即可求出值.
解答 解:(1)原式=m2-4mn+4n2-n2
=(m-2n)2-n2
=(m-2n+n)(m-2n-n)
=(m-n)(m-3n);
(2)原式=$\frac{x}{x-y}$+$\frac{{y}^{2}}{x(x-y)^{2}}$•$\frac{-(x+y)(x-y)}{y(x+y)}$
=$\frac{x}{x-y}$-$\frac{y}{x(x-y)}$
=$\frac{{x}^{2}-y}{x(x-y)}$,
当x=1,y=3时,原式=1.
点评 此题考查了分式的化简求值,以及配方法的应用,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
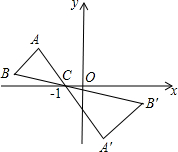 如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设B′的坐标是(3,-1),则点B的坐标是(-3,$\frac{1}{2}$).
如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设B′的坐标是(3,-1),则点B的坐标是(-3,$\frac{1}{2}$). 如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,6)的对应点A′的坐标是(6,2).
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,6)的对应点A′的坐标是(6,2).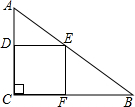 如图,正方形CDEF内接于Rt△ABC,点D、E、F分别在边AC、AB和BC上,当AD=2,BF=3时,正方形CDEF的面积是6.
如图,正方形CDEF内接于Rt△ABC,点D、E、F分别在边AC、AB和BC上,当AD=2,BF=3时,正方形CDEF的面积是6.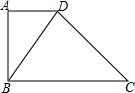 如图,已知四边形ABCD中,∠A=90°,AD∥BC.
如图,已知四边形ABCD中,∠A=90°,AD∥BC. 李先生准备在永川某小区内购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是8000元/m2,面积如图所示(单位:m,卫生间的宽未定,设宽为xm),售房部为李先生提供了以下两种优惠方案:
李先生准备在永川某小区内购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是8000元/m2,面积如图所示(单位:m,卫生间的宽未定,设宽为xm),售房部为李先生提供了以下两种优惠方案: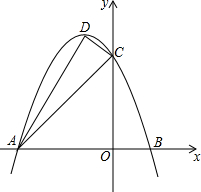 如图抛物线y=ax2+bx+3与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,顶点为D,连接AC、CD、AD.
如图抛物线y=ax2+bx+3与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,顶点为D,连接AC、CD、AD.