题目内容
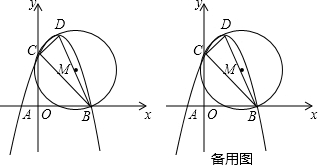
13.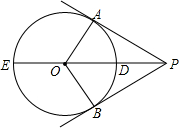 如图,PA、PB是⊙O的两条切线,切点分别为A、B,直线OP交⊙O于点D、E.
如图,PA、PB是⊙O的两条切线,切点分别为A、B,直线OP交⊙O于点D、E.(1)求证:△PAO≌△PBO;
(2)已知PA=4,PD=2,求⊙O的半径.
分析 (1)根据切线长定理得到PA=PB,∠OPA=∠OPB,再根据切线的性质得到∠OAP=∠OBP=90°,然后根据三角形全等的判定方法即可得到结论;
(2)由PA⊙O的切线,得到OA⊥PA,设⊙O的半径为r,则OA=OD=r,在Rt△OAP中根据勾股定理得到r2+42=(r+2)2,然后解方程即可.
解答 (1)证明:∵PA,PB是⊙O的切线,
∴∠PAO=∠PBO=90°,
在Rt△PAO与Rt△PBO中,$\left\{\begin{array}{l}{OA=OB}\\{OP=OP}\end{array}\right.$,
∴Rt△PAO≌Rt△PBO;
(2)解:∵PA⊙O的切线,
∴OA⊥PA,
在Rt△OAP中,设⊙O的半径为r,则OP=OD+PD=r+2,
∵OA2+PA2=OP2,
∴r2+42=(r+2)2,解得r=3,
即半径OA的长为3.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径,也考查了切线长定理、全等三角形的判定和勾股定理,熟练掌握切线的性质:圆的切线垂直于经过切点的半径是解题的关键.

练习册系列答案
相关题目
5.如果三角形的三边长分别为4、6、8,那么连结该三角形三边中点所得三角形的周长是( )
| A. | 6 | B. | 9 | C. | 10 | D. | 12 |
2.下列说法正确的是( )
| A. | 同位角相等 | |
| B. | 对顶角相等 | |
| C. | 两条直线被第三条直线所截,内错角相等 | |
| D. | 两条平行直线被第三条直线所截,同旁内角相等 |
3.下列命题中正确的是( )
| A. | 全等三角形的高相等 | B. | 全等三角形的中线相等 | ||
| C. | 全等三角形的角平分线相等 | D. | 全等三角形对应角相等 |
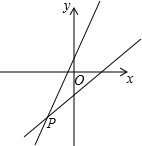 一次函数y=3x+b和y=ax-3的图象如图所示,其交点为P(-2,-5),则不等式3x+b>ax-3的解集在数轴上表示正确的是( )
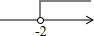
一次函数y=3x+b和y=ax-3的图象如图所示,其交点为P(-2,-5),则不等式3x+b>ax-3的解集在数轴上表示正确的是( )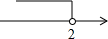

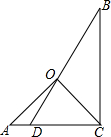 如图,一副三角板△AOC和△BCD如图摆放,则∠AOB=165°.
如图,一副三角板△AOC和△BCD如图摆放,则∠AOB=165°.