题目内容
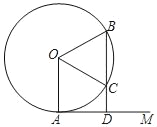
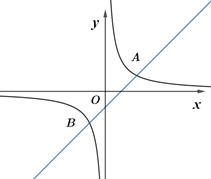
【题目】已知：如图1，在平面直角坐标系中，直线1：y＝﹣x+4与坐标轴分别相交于点A、B与l2：y＝
x相交于点C．
（1）求点C的坐标；
（2）若平行于y轴的直线x＝a交于直线1于点E，交直线l2于点D，交x轴于点M，且ED＝2DM，求a的值；
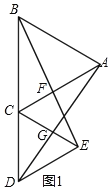
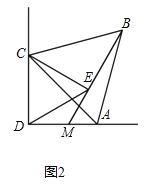
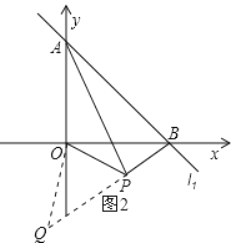
（3）如图2，点P是第四象限内一点，且∠BPO＝135°，连接AP，探究AP与BP之间的位置关系，并证明你的结论．
【答案】（1）（3，1）；（2）a＝2或6；（3）AP⊥BP，证明见解析.
【解析】
（1）联立两直线解析式得到方程组，求出方程组的解即可确定出C的坐标；
（2）将x=1代入两直线方程求出对应y的值，确定出D与E的纵坐标，即OD与OE的长，由OE﹣OD求出DE的长，根据ED=2DM，求出MN的长，将x=a代入两直线方程，求出M与N对应的横坐标，相减的绝对值等于MN的长列出关于a的方程，求出方程的解即可求出a的值；
（3）AP⊥BP，理由为：过O作OQ⊥OP，交BP的延长线于点Q，由∠BPO为135°，得到∠OPQ为45°，又∠POQ为直角，可得出三角形OPQ为等腰直角三角形，再利用两对对应边成比例且夹角相等的两三角形相似得到三角形AOP与三角形BOQ相似，由相似三角形的对应角相等得到∠APO=∠BQO=45°，由∠BPO﹣∠APO得到∠APB为直角，即AP⊥BP．
（1）联立两直线解析式得：
，解得：
，则C坐标为（3，1）；
（2）由题意：M（a，0）D（a，
a） E（a，﹣a+4）．
∵DE=2DM，∴|a﹣（﹣a+4）|=2|a|，解得：a=2或6．
（3）如图2中，过O作OQ⊥OP，交BP的延长线于点Q，可得∠POQ=90°．
∵∠BPO=135°，∴∠OPQ=45°，∴∠Q=∠OPQ=45°，∴△POQ为等腰直角三角形，∴OP=OQ．
∵∠AOB=∠POQ=90°，∴∠AOB+∠BOP=∠POQ+∠POB，即∠AOP=∠BOQ．
∵OA=OB=4，∴
，∴△AOP∽△BOQ，∴∠APO=∠BQO=45°，∴∠APB=∠BPO﹣∠APO=90°，则AP⊥BP．
