题目内容
16．
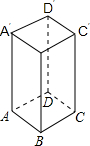如图，正四棱柱的底面边长为5cm，侧棱长为8cm，一只蚂蚁欲从正四棱柱底面上的顶点 A沿棱柱的表面到顶点C′处吃食物．那么它需要爬行的最短路程的长是多少？
分析 将正四棱柱展开，利用勾股定理解答，得到两个结果，取其值最小者即为所求答案．
解答 解：分两种情况：①AC′=$\sqrt{A{B}^{2}+BC{′}^{2}}$=$\sqrt{194}$（cm）；
②AC′=$\sqrt{A{C}^{2}+CC{′}^{2}}$=2$\sqrt{41}$（cm）．
因为 2$\sqrt{41}$＜$\sqrt{194}$，所以最短路程为2$\sqrt{41}$cm．
点评 此题考查了长方体的展开---最短路径问题，将图形展开构造直角三角形求出斜边长是解题的关键．
练习册系列答案
相关题目
如图所示，PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，CD∥AB交⊙O于D，∠P=40°．
