题目内容
1. 如图所示,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,CD∥AB交⊙O于D,∠P=40°.
如图所示,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,CD∥AB交⊙O于D,∠P=40°.(1)求∠CAB的度数.
(2)求证:四边形ABCD是矩形.
(3)如果PA=13,CD=10,求⊙O的直径.
分析 (1)首先求出∠AOB的度数,再根据等腰三角形的性质即可解决问题.
(2)由△ACB≌△CAD,推出AB=CD,由AB∥CD,推出四边形ABCD是平行四边形,由∠D=90°,即可解决问题.
(3)在RT△APE中,利用勾股定理求出PE,再由△PAE∽△POA求出OA即可解决问题.
解答 (1)解:连接OB,
∵PA、PB是切线,
∴OA⊥PA,OB⊥PB,
∴∠PAO=∠PBO=90°,
∵∠APB=40°,
∴∠AOB=360°-∠APB-∠PAO-∠PBO=360°-40°-90°-90°=140°,
∵OA=OB,
∴∠CAB=∠OBA=(180°-∠AOB)÷2=20°.
(2)证明:∵AC是⊙O直径,
∴∠CBA=∠D=90°,
∵AB∥CD,
∠CAB=∠ACO,
∵AC=CA,
∴△CAB≌△ACD,
∴AB=CD,
∴四边形ABCD是平行四边形,
∵∠D=90°,
∴四边形ABCD是矩形.
(3)解:连接PO交AB于点E,
∵四边形ABCD是矩形,
∴AB=CD=10,
∵PA、PB是切线,
∴PA=PB,∠APO=∠OPB,
∴OP⊥AB,AE=EB=5,
∴∠PEA=90°,
∴PE=$\sqrt{P{A}^{2}-A{E}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∴∠OAB=∠AEP=90°,∠OPA=∠APE,
∴△OPA∽△APE,
∴$\frac{OA}{AE}$=$\frac{PA}{PE}$,
∴$\frac{OA}{5}$=$\frac{13}{12}$,
∴OA=$\frac{65}{12}$,
∴⊙O的直径AC=2OA=$\frac{65}{6}$.
点评 本题考查切线的性质、矩形、平行四边形的判定和性质、全等三角形判定的判定和性质、相似三角形的判定和性质等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案| A品牌电脑的数量 (单位:台) | B品牌课桌的数量 (单位:张) | 总价 (单位:元) | |
| 第一次 | 10 | 200 | 70000 |
| 第二次 | 15 | 100 | 75000 |
(2)在“五•一”黄金周期间,经销商对一次性购买量大的客户打折优惠:一次性购买A品牌电脑不少于50台,按9折优惠;一次性购买B品牌课桌不少于450张,按8折优惠.如果学校再次购买A品牌电脑和B品牌课桌若干,恰好花去24万元,并且均享受了优惠,那么学校可能有哪几种购买方案?
 已知:正方形ABCD中,点E、F、G、H分别在AB、BC、CD、DA上,且AE=BF=CG=DH,
已知:正方形ABCD中,点E、F、G、H分别在AB、BC、CD、DA上,且AE=BF=CG=DH,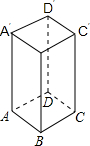 如图,正四棱柱的底面边长为5cm,侧棱长为8cm,一只蚂蚁欲从正四棱柱底面上的顶点 A沿棱柱的表面到顶点C′处吃食物.那么它需要爬行的最短路程的长是多少?
如图,正四棱柱的底面边长为5cm,侧棱长为8cm,一只蚂蚁欲从正四棱柱底面上的顶点 A沿棱柱的表面到顶点C′处吃食物.那么它需要爬行的最短路程的长是多少?
 如图,AD∥BC,在AB上取一点M,过M画MN∥BC交CD于N,并说明MN与AD的位置关系,为什么?
如图,AD∥BC,在AB上取一点M,过M画MN∥BC交CD于N,并说明MN与AD的位置关系,为什么?