题目内容
14.若关于x的一元二次方程(m-4)x2+(2m-1)x+1=0的两个实数根的倒数和为s,则s的取值范围是s≠-7.分析 m-4≠0,且△总是大于0,则m的范围为m≠4,再根据根与系数的关系得到x1+x2=-$\frac{2m-1}{m-4}$,x1x2=$\frac{1}{m-4}$,则s=$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=-2m+1,然后根据m的范围确定s的范围.
解答 解:根据题意得m-4≠0且△=(2m-1)2-4(m-4)≥0,解得m≠4,
x1+x2=-$\frac{2m-1}{m-4}$,x1x2=$\frac{1}{m-4}$,
s=$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=-2m+1,
由于m≠4,
所以s≠-7.
故答案为s≠-7.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
 如图,在△ABC中.△ACB=90°,点0为三条角平分线的交点,0D⊥BC于D,0E⊥AC于E,0F⊥AB于F,且AB=10cm,CB=6cm,CA=8cm,求0D的长.
如图,在△ABC中.△ACB=90°,点0为三条角平分线的交点,0D⊥BC于D,0E⊥AC于E,0F⊥AB于F,且AB=10cm,CB=6cm,CA=8cm,求0D的长.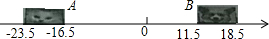 七年级小贝在-张纸上画了-条数轴,妹妹不知它有什么用,就在上面画了一只小猫和一只小狗,于是数轴上标的数字有的看不到了,请根据数轴回答下列问题:
七年级小贝在-张纸上画了-条数轴,妹妹不知它有什么用,就在上面画了一只小猫和一只小狗,于是数轴上标的数字有的看不到了,请根据数轴回答下列问题: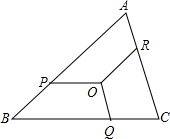 如图,点O是△ABC内一点,点P、Q、R分别在边AB、BC、CA上,且OP∥BC,OQ∥CA,OR∥AB,OP=OQ=OR,BC=a,CA=b,AB=c,求OP的长.
如图,点O是△ABC内一点,点P、Q、R分别在边AB、BC、CA上,且OP∥BC,OQ∥CA,OR∥AB,OP=OQ=OR,BC=a,CA=b,AB=c,求OP的长.