题目内容
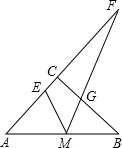 如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=8,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.
如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=8,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.(1)在不添加字母和线段的情况下写出图中一定相似的三角形,并证明其中的一对;
(2)连接结EG,当AE=6时,求EG的长.
考点:相似三角形的判定与性质
专题:
分析:(1)证明∠A=∠B=45°,∠AEM=∠BMG,得到△AME∽△BGM.
(2)由△AME∽△BGM,列出比例式,结合∠A=∠EMG=45°,得到△AME∽△MGE,这是解决该题的关键结论;根据余弦定理求出ME的长度,列出关于线段GE的比例式即可解决问题.
(2)由△AME∽△BGM,列出比例式,结合∠A=∠EMG=45°,得到△AME∽△MGE,这是解决该题的关键结论;根据余弦定理求出ME的长度,列出关于线段GE的比例式即可解决问题.
解答: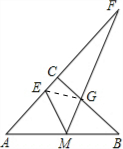 解:(1)△AME∽△BGM.
解:(1)△AME∽△BGM.
证明如下:
∵∠ACB=90°,AC=BC,
∴∠A=∠B=45°;而∠EMG=45°,
∴∠AEM+∠AME=∠AME+∠BMG=135°,
∴∠AEM=∠BMG,
∴△AME∽△BGM.
(2)∵∠ACB=90°,AC=BC=8,
∴由勾股定理得:AB2=64+64,
∴AB=8
;
∴AM=BM=4
;
∵△AME∽△BGM,
∴ME:MG=AE:BM,而AM=BM,
∴ME:MG=AE:AM,
∴ME:AE=MG:AM,而∠A=∠EMG=45°,
∴△AME∽△MGE,
∴ME:GE=AE:ME,
GE=
;
由余弦定理得:ME2=(4
)2+62-2×4
×6•cos45°=20,
∴ME=2
,GE=
.
 解:(1)△AME∽△BGM.
解:(1)△AME∽△BGM.证明如下:
∵∠ACB=90°,AC=BC,
∴∠A=∠B=45°;而∠EMG=45°,
∴∠AEM+∠AME=∠AME+∠BMG=135°,
∴∠AEM=∠BMG,
∴△AME∽△BGM.
(2)∵∠ACB=90°,AC=BC=8,
∴由勾股定理得:AB2=64+64,
∴AB=8
| 2 |
∴AM=BM=4
| 2 |
∵△AME∽△BGM,
∴ME:MG=AE:BM,而AM=BM,
∴ME:MG=AE:AM,
∴ME:AE=MG:AM,而∠A=∠EMG=45°,
∴△AME∽△MGE,
∴ME:GE=AE:ME,
GE=
| ME2 |
| AE |
由余弦定理得:ME2=(4
| 2 |
| 2 |
∴ME=2
| 5 |
| 10 |
| 3 |
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是深入观察图形结构特点,找出图形中隐含的相等或相似关系;大胆猜测推理,科学解答论证.

练习册系列答案
相关题目
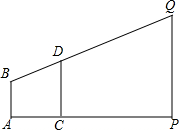 如图所示,旗杆顶部Q,标杆顶部D,观测者的眼睛B在同一直线上,测得观测者的脚到旗杆底部的距离AP=75m,观测者的脚到标杆底部的距离AC=2.5m,若AB=1.5m,标杆CD的高为2m,那么旗杆有多高.
如图所示,旗杆顶部Q,标杆顶部D,观测者的眼睛B在同一直线上,测得观测者的脚到旗杆底部的距离AP=75m,观测者的脚到标杆底部的距离AC=2.5m,若AB=1.5m,标杆CD的高为2m,那么旗杆有多高. 如图,∠B=∠D,∠BAC=∠DAC.求证:AB=AD.
如图,∠B=∠D,∠BAC=∠DAC.求证:AB=AD.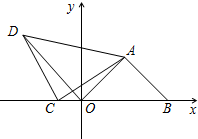 如图,在平面直角坐标系中,△AOB为等腰直角三角形,AB=OA,B(8,0),C为x轴负半轴上一动点,以AC为直角边作等腰直角△ACD,∠ACD=90°,连OD.
如图,在平面直角坐标系中,△AOB为等腰直角三角形,AB=OA,B(8,0),C为x轴负半轴上一动点,以AC为直角边作等腰直角△ACD,∠ACD=90°,连OD. 如图,已知线段AB的两个端点在直角坐标系中的坐标分别是A(m,m),B(2n,n),以原点O为位似中心,相似比为
如图,已知线段AB的两个端点在直角坐标系中的坐标分别是A(m,m),B(2n,n),以原点O为位似中心,相似比为