题目内容
 如图,已知线段AB的两个端点在直角坐标系中的坐标分别是A(m,m),B(2n,n),以原点O为位似中心,相似比为
如图,已知线段AB的两个端点在直角坐标系中的坐标分别是A(m,m),B(2n,n),以原点O为位似中心,相似比为| 1 |
| 2 |
考点:位似变换,坐标与图形性质
专题:计算题
分析:由于在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k,则把点A和点B的坐标都乘以
即可得到点A′和点B′的坐标,再利用两点间的距离公式计算点A到原点O的距离.
| 1 |
| 2 |
解答:解:∵A(m,m),B(2n,n),
而位似中心为原点,相似比为
,
∴A′(
m,
m),B′(n,
n);
点A到原点O的距离=
=
m.
故答案为(
m,
m),(n,
n);
m.
而位似中心为原点,相似比为
| 1 |
| 2 |
∴A′(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点A到原点O的距离=
| m2+m2 |
| 2 |
故答案为(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
点评:本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法中,正确的是( )
| A、一个有理数的平方总是正数 |
| B、最大的负数是-1 |
| C、有理数包括正有理数和负有理数 |
| D、没有最大的正数,也没有最小的负数 |
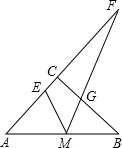 如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=8,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.
如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=8,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F. 如图,矩形ABCD中,CF⊥BD于F,点E恰好是AD的中点,AD=4,则CD的长为
如图,矩形ABCD中,CF⊥BD于F,点E恰好是AD的中点,AD=4,则CD的长为