题目内容
 如图,等边△ABC,点D、E、F分别是BC、CA、AB的中点,则S△DEF:S△ABC=
如图,等边△ABC,点D、E、F分别是BC、CA、AB的中点,则S△DEF:S△ABC=考点:等边三角形的性质
专题:几何图形问题
分析:利用三角形中位线定理得出EF
BC,DF
AC,ED
BA,则△DFE∽△ACB,进而利用相似三角形的性质得出答案.
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
解答:解:∵等边△ABC,点D、E、F分别是BC、CA、AB的中点,
∴EF
BC,DF
AC,ED
BA,
∴△DFE∽△ACB,
∴
=
,
∴S△DEF:S△ABC=1:4.
故答案为:1:4.
∴EF
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
∴△DFE∽△ACB,
∴
| EF |
| BC |
| 1 |
| 2 |
∴S△DEF:S△ABC=1:4.
故答案为:1:4.
点评:此题主要考查了等边三角形的性质和相似三角形的判定与性质,得出△DFE∽△ACB是解题关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
下列式子正确的是( )
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
 如图,△ABC的顶点是正方形网格的格点,则tanA的值为
如图,△ABC的顶点是正方形网格的格点,则tanA的值为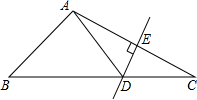 如图,△ABC中,DE是AC的垂直平分线,AE=2.5cm,△ABD的周长为15cm,则△ABC的周长是
如图,△ABC中,DE是AC的垂直平分线,AE=2.5cm,△ABD的周长为15cm,则△ABC的周长是 如图,△ABC是等边三角形,点D是AB的三等分点,且
如图,△ABC是等边三角形,点D是AB的三等分点,且 如图,在等腰直角三角形ABC中,AD⊥BC,PE⊥AB,PF⊥AC,则△DEF是
如图,在等腰直角三角形ABC中,AD⊥BC,PE⊥AB,PF⊥AC,则△DEF是