题目内容
16.三角形两边长分别为3和5,第三边是方程x2-6x+8=0的一个解,则这个三角形的面积是6.分析 先解方程求出方程的解,得出两种情况,看看是否符合三角形三边关系定理,再求出即可.
解答 解:解方程x2-6x+8=0得:x1=4,x2=2,
①当三角形的三边为3,4,5时,符合三角形三边关系定理,
∵32+42=52,
∴此时三角形为直角三角形,
∴这个三角形的面积为$\frac{1}{2}×3×4$=6;
②当三角形的三边为3,2,5时,不符合三角形三边关系定理,此时三角形不存在;
故答案为:6.
点评 本题考查了勾股定理的逆定理,三角形的面积,三角形三边关系定理,解一元二次方程的应用,能求出符合的所有情况是解此题的关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
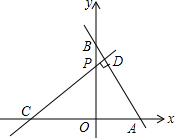 如图.在平面直角坐标系中,点C、点A为x轴上两点,OA、OC的长是方程y=x2-7x+12=0的两个根(OC>OA).点B在y轴上,CD⊥AB交y轴于点P,且CP=AB.
如图.在平面直角坐标系中,点C、点A为x轴上两点,OA、OC的长是方程y=x2-7x+12=0的两个根(OC>OA).点B在y轴上,CD⊥AB交y轴于点P,且CP=AB.
 如图是一个圆台及其主视图,你能把它的俯视图和左视图补上吗?
如图是一个圆台及其主视图,你能把它的俯视图和左视图补上吗?