题目内容
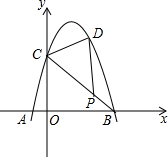 如图,抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,点P的坐标为
如图,抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,点P的坐标为考点:二次函数的性质
专题:
分析:把点A、C的坐标代入抛物线解析式求出b、c的值,从而得到抛物线的解析式,再求出点B的坐标,然后利用待定系数法求出直线BC的解析式,当与BC平行的直线与抛物线有且只有一个交点时,点D到BC的距离最大,此时△BDC的面积最大,然后联立直线与抛物线解析式,消掉y得到关于x的一元二次方程,利用根与系数的关系求出x的值,即可得到点D的横坐标,然后代入直线BC的解析式求出点P的纵坐标,即可得解.
解答: 解:(1)∵抛物线y=-x2+bx+c经过点A(-1,0),C(0,3),
解:(1)∵抛物线y=-x2+bx+c经过点A(-1,0),C(0,3),
∴
,
解得
,
∴y=-x2+2x+3,
令y=0,则-x2+2x+3=0,
解得x1=-1,x2=3,
∴点B的坐标为(3,0),
设直线BC的解析式为y=kx+b,
则
,
解得
,
所以,直线BC的解析式为y=-x+3,
过点D作BC的平行直线,设解析式为y=-x+d,
联立
,
消掉y得,-x2+2x+3=-x+d,
整理得,x2-3x-3+d=0,
当△=0时,方程有两个相等的实数根,此时点D到BC的距离最大,△BDC的面积最大,
所以,x=-
=
,
∵PD∥y轴,
∴点P的横坐标为
,
此时y=-
+3=
,
∴点P的坐标为(
,
).
故答案为:(
,
).
 解:(1)∵抛物线y=-x2+bx+c经过点A(-1,0),C(0,3),
解:(1)∵抛物线y=-x2+bx+c经过点A(-1,0),C(0,3),∴
|
解得
|
∴y=-x2+2x+3,
令y=0,则-x2+2x+3=0,
解得x1=-1,x2=3,
∴点B的坐标为(3,0),
设直线BC的解析式为y=kx+b,
则
|
解得
|
所以,直线BC的解析式为y=-x+3,
过点D作BC的平行直线,设解析式为y=-x+d,
联立
|
消掉y得,-x2+2x+3=-x+d,
整理得,x2-3x-3+d=0,
当△=0时,方程有两个相等的实数根,此时点D到BC的距离最大,△BDC的面积最大,
所以,x=-
| -3 |
| 2×1 |
| 3 |
| 2 |
∵PD∥y轴,
∴点P的横坐标为
| 3 |
| 2 |
此时y=-
| 3 |
| 2 |
| 3 |
| 2 |
∴点P的坐标为(
| 3 |
| 2 |
| 3 |
| 2 |
故答案为:(
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题是二次函数的性质,主要考查了待定系数法求函数解析式(二次函数解析式与直线解析式),联立两函数解析式求交点坐标,平行直线的解析式的k值相等,相似三角形对应边成比例的性质,二次函数的最大值问题,综合性较强,难度较大.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
某年,一些国家的服务出口额比上年的增长率如下.美国-3.4%,德国-0.9%,中国2.8%,日本-7.3%,其中增长率最低的是( )
| A、美国 | B、德国 | C、中国 | D、日本 |
若x2-4x+p=(x+q)2,则p、q的值分别是( )
| A、4、2 | B、4、-2 |
| C、-4、-2 | D、-4、2 |
下列说法不正确的是( )
| A、0既不是正数,也不是负数 |
| B、0的绝对值是0 |
| C、一个有理数不是整数就是分数 |
| D、1是绝对值最小的正数 |
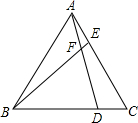 如图,已知△ABC为等边三角形,点D、E分别在边BC、AC上,且AE=CD,AD与BE交于点F.
如图,已知△ABC为等边三角形,点D、E分别在边BC、AC上,且AE=CD,AD与BE交于点F.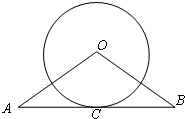 如图,AB与⊙O相切于C,∠A=∠B,⊙O的半径为6,OA=10,求AB的长.
如图,AB与⊙O相切于C,∠A=∠B,⊙O的半径为6,OA=10,求AB的长. 一个水池,装有一个进水管和一个出水管(进、出水管都是匀速的),水池内水位高为s(米)与注水时间t(分)之间的函数关系如图所示,结合图象回答下列问题:
一个水池,装有一个进水管和一个出水管(进、出水管都是匀速的),水池内水位高为s(米)与注水时间t(分)之间的函数关系如图所示,结合图象回答下列问题: