题目内容
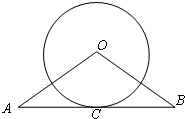 如图,AB与⊙O相切于C,∠A=∠B,⊙O的半径为6,OA=10,求AB的长.
如图,AB与⊙O相切于C,∠A=∠B,⊙O的半径为6,OA=10,求AB的长.考点:切线的性质
专题:
分析:连接OC,由切线的性质可得OC⊥AB,由∠A=∠B可知OA=OB,由等腰三角形的三线合一的性质得到OC也是AB的中线,从而得到AC=BC;再根据勾股定理求得AC的长,就求得了AB的长.
解答:解:连接OC.

∵AB与⊙O相切于点C,
∴OC⊥AB,
又∵∠A=∠B,
∴OA=OB,
∴AC=BC=
AB,
在Rt△AOC中,AC=
=
=8,
∴AB=2AC=2×8=16.

∵AB与⊙O相切于点C,
∴OC⊥AB,
又∵∠A=∠B,
∴OA=OB,
∴AC=BC=
| 1 |
| 2 |
在Rt△AOC中,AC=
| OA2-OC2 |
| 102-62 |
∴AB=2AC=2×8=16.
点评:此题主要考查学生对切线的性质及勾股定理的理解及运用.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
下列二次根式中,属于最简二次根式的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
某机械厂现加工一批零件,直径尺寸要求是40±0.03(单位mm),则直径是下列各数值的产品中合格的是( )
| A、39.90 |
| B、39.94 |
| C、40.01 |
| D、40.04 |
 如图,在△ABC中,∠BAC=90°,AD⊥BC于D,AE平分∠DAC,∠B=50°,求∠1.
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,AE平分∠DAC,∠B=50°,求∠1.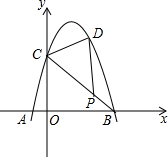 如图,抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,点P的坐标为
如图,抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,点P的坐标为