题目内容
8.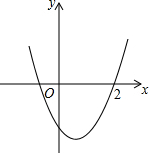 若将图中的抛物线y=x2-2x+c向上平移,使它经过点(2,0),则此时的抛物线位于x轴下方的图象对应x的取值范围是0<x<2.
若将图中的抛物线y=x2-2x+c向上平移,使它经过点(2,0),则此时的抛物线位于x轴下方的图象对应x的取值范围是0<x<2.
分析 设平移后的抛物线解析式为y=x2-2x+c+b,把点A的坐标代入进行求值即可得到c+b的值,然后求得抛物线与x轴的交点坐标,即可得到结论.
解答 解:设平移后的抛物线解析式为y=x2-2x+c+b,
把A(2,0)代入,得
0=c+b,
解得c+b=0,
则该函数解析式为y=x2-2x.
当y=0时,x2-2x=0,
解得:x1=0,x2=2,
∴此时的抛物线位于x轴下方的图象对应x的取值范围是:0<x<2,
故答案为:0<x<2.
点评 主要考查了函数图象的平移,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程求抛物线与坐标轴的交点.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
16.若一个三角形的三边长分别为5、7、x-2,则x的取值范围是( )
| A. | 0<x<14 | B. | 4<x<14 | C. | 0<x<10 | D. | 2<x<10 |
13.若a,b为两质数且相差2,则ab+1之值可能为下列何者( )
| A. | 392 | B. | 402 | C. | 412 | D. | 422 |
 尺规作图.
尺规作图.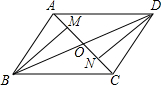 已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,M、N分别是OA、OC的中点,求证:BM∥DN.
已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,M、N分别是OA、OC的中点,求证:BM∥DN.
 如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.