题目内容
20.计算:(1)$\sqrt{8}$+3$\sqrt{\frac{1}{3}}$-$\frac{1}{\sqrt{2}}$-$\sqrt{\frac{3}{4}}$;
(2)(3$\sqrt{2}$-2$\sqrt{3}$)2-(3$\sqrt{2}$+2$\sqrt{3}$)2.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先利用平方差公式进行,然后把括号内合并后进行二次根式的乘法运算.
解答 解:(1)原式=2$\sqrt{2}$+$\sqrt{3}$-$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{2}$
=$\frac{3\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}$;
(2)原式=(3$\sqrt{2}$-2$\sqrt{3}$+3$\sqrt{2}$+2$\sqrt{3}$)(3$\sqrt{2}$-2$\sqrt{3}$-3$\sqrt{2}$-2$\sqrt{3}$)
=6$\sqrt{2}$•(-4$\sqrt{3}$)
=-24$\sqrt{6}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
5.资料显示2013年上半年台州市全年财政总收入为242亿元,将242亿元保留2个有效数字可表示为( )
| A. | 240000000000元 | B. | 2.42×108元 | C. | 2.4×109元 | D. | 2.4×1010元 |
10.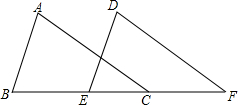 如图,在△ABC中,BC=5,∠A=70°,∠B=75°,把△ABC沿直线BC的方向平移到△DEF的位置,若CF=3,则下列结论中错误的是( )
如图,在△ABC中,BC=5,∠A=70°,∠B=75°,把△ABC沿直线BC的方向平移到△DEF的位置,若CF=3,则下列结论中错误的是( )
 如图,在△ABC中,BC=5,∠A=70°,∠B=75°,把△ABC沿直线BC的方向平移到△DEF的位置,若CF=3,则下列结论中错误的是( )
如图,在△ABC中,BC=5,∠A=70°,∠B=75°,把△ABC沿直线BC的方向平移到△DEF的位置,若CF=3,则下列结论中错误的是( )| A. | BE=3 | B. | ∠F=35° | C. | DF=5 | D. | AB∥DE |
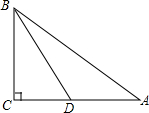 如图,△ABC为直角三角形,∠C=90°,AC=4,CB=3,AB=5,BD为△ABC的中线,AE平分∠BAC交BD于E,则E到BC的距离为$\frac{10}{7}$.
如图,△ABC为直角三角形,∠C=90°,AC=4,CB=3,AB=5,BD为△ABC的中线,AE平分∠BAC交BD于E,则E到BC的距离为$\frac{10}{7}$.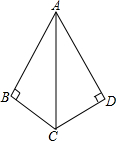 已知如图,∠B=∠D=90°,要使△ABC≌△ADC,还需要补充一个条件,那么这个条件可以是AB=AD(答案不唯一).
已知如图,∠B=∠D=90°,要使△ABC≌△ADC,还需要补充一个条件,那么这个条件可以是AB=AD(答案不唯一).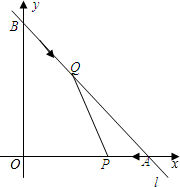 如图,已知直线l的函数表达式为y=-$\frac{4}{3}$x+8,且l与x轴、y轴分别交于A、B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒.
如图,已知直线l的函数表达式为y=-$\frac{4}{3}$x+8,且l与x轴、y轴分别交于A、B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒.