题目内容
1.多项式x2+mx-12因式分解可得(x+4)(x+n),则mn的值为-3.分析 根据多项式x2+mx-12因式分解可得(x+4)(x+n),得出x2+mx-12=x2+(4+n)x+4n,即可求出m,n的值,从而得出mn的值.
解答 解:∵多项式x2+mx-12因式分解可得(x+4)(x+n),
∴x2+mx-12=x2+(4+n)x+4n,
∴$\left\{\begin{array}{l}{m=4+n}\\{4n=-12}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m=1}\\{n=-3}\end{array}\right.$
∴mn=-3.
故答案为:-3.
点评 此题考查了因式分解的意义;关键是根据因式分解的意义求出m,n的值,是一道基础题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
12.下列关于平角和周角的说法正确的是( )
| A. | 平角是一条线段 | B. | 周角是一条射线 | ||
| C. | 两个锐角的和不一定小于平角 | D. | 反向延长射线OA,就形成一个平角 |
16.计算2$\sqrt{\frac{1}{2}}$$+3\sqrt{\frac{1}{3}}$$-\sqrt{8}$的结果是( )
| A. | $\sqrt{3}-\sqrt{2}$ | B. | $\sqrt{2}-\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3$\sqrt{2}$ |
6.计算(200-2)(200+2)的结果是( )
| A. | 39998 | B. | 39996 | C. | 29996 | D. | 39992 |
11.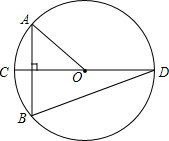 如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )
如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )
 如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )
如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
 如图,在平面直角坐标系中,点A的坐标为(0,2),点p的坐标为(m,0)且m>0,一开口向上的抛物线以P为顶点,且经过点A.
如图,在平面直角坐标系中,点A的坐标为(0,2),点p的坐标为(m,0)且m>0,一开口向上的抛物线以P为顶点,且经过点A.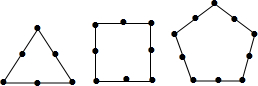 墨墨用黑色的棋子摆各种正多边形,如图所示,他摆正三角形的时候用了6个棋子,摆正方形的时候用了8个棋子,摆正五边形的时候用了10个棋子,以此类推,当墨墨摆完正十二边形时,共用了150个棋子.
墨墨用黑色的棋子摆各种正多边形,如图所示,他摆正三角形的时候用了6个棋子,摆正方形的时候用了8个棋子,摆正五边形的时候用了10个棋子,以此类推,当墨墨摆完正十二边形时,共用了150个棋子.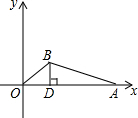 如图,在直角坐标系中,点A的坐标是(12,0),动直线OB与AB相交于点B,且BD⊥x轴于D,BD=3,则△OAB的周长的最小值是12+6$\sqrt{5}$.
如图,在直角坐标系中,点A的坐标是(12,0),动直线OB与AB相交于点B,且BD⊥x轴于D,BD=3,则△OAB的周长的最小值是12+6$\sqrt{5}$.