题目内容
如图,已知在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=11,BC=13,AB=12.动点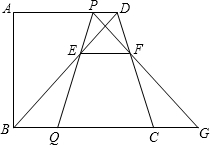 P、Q分别在边AD和BC上,且BQ=2DP.线段PQ与BD相交于点E,过点E作EF∥BC,交CD于点F,射线PF交BC的延长线于点G,设DP=x.
P、Q分别在边AD和BC上,且BQ=2DP.线段PQ与BD相交于点E,过点E作EF∥BC,交CD于点F,射线PF交BC的延长线于点G,设DP=x.(1)求
| DF | CF |
(2)当点P运动时,试探究四边形EFGQ的面积是否会发生变化?如果发生变化,请用x的代数式表示四边形EFGQ的面积S;如果不发生变化,请求出这个四边形的面积S.
(3)当△PQG是以线段PQ为腰的等腰三角形时,求x的值.
分析:(1)由平行线分线段成比例即可求解其比值;
(2)点P在AD上运动时,由平行线分线段成比例的性质可得EF与QG的比例始终是1:3,且BQ=CG,所以其面积为定值,进而求出其面积即可;
(3)以线段PQ为腰,则可能是PQ=PG,也可能是PQ=QG,所以分开求解即可.
(2)点P在AD上运动时,由平行线分线段成比例的性质可得EF与QG的比例始终是1:3,且BQ=CG,所以其面积为定值,进而求出其面积即可;
(3)以线段PQ为腰,则可能是PQ=PG,也可能是PQ=QG,所以分开求解即可.
解答:解:(1)在梯形ABCD中,
∵AD∥BC,∴
=
.
∵EF∥BC,∴
=
.
又∵BQ=2DP,∴
=
.
(2)不发生变化.
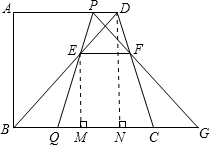 作EM⊥BC,垂足为点M,
作EM⊥BC,垂足为点M,
在△BCD中,
∵EF∥BC,
∴
=
=
.
而BC=13,
∴EF=
.
又∵PD∥CG,
∴
=
=
.
∴CG=2PD.
∴CG=BQ,即QG=BC=13.
作DN⊥BC,垂足为点N.
∴
=
=
=
,
而AB=12,
∴可求得EM=8.
∴S=
×(
+13)×8=
.
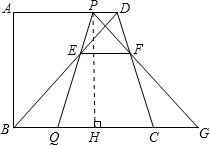
(3)作PH⊥BC,垂足为点H.
(i)当PQ=PG时,QH=GH=
.
∴2x+
=11-x.
解得x=
.
(ii)当PQ=GQ时,PQ=
=13.
解得x=2或x=
.
综上所述,当△PQG是以PQ为腰的等腰三角形时,x的值为
、2或
.
∵AD∥BC,∴
| DE |
| BE |
| DP |
| BQ |
∵EF∥BC,∴
| DE |
| BE |
| DF |
| CF |
又∵BQ=2DP,∴
| DF |
| CF |
| 1 |
| 2 |
(2)不发生变化.
 作EM⊥BC,垂足为点M,
作EM⊥BC,垂足为点M,在△BCD中,
∵EF∥BC,
∴
| EF |
| BC |
| DE |
| DB |
| 1 |
| 3 |
而BC=13,
∴EF=
| 13 |
| 3 |
又∵PD∥CG,
∴
| PD |
| CG |
| DF |
| CF |
| 1 |
| 2 |
∴CG=2PD.
∴CG=BQ,即QG=BC=13.
作DN⊥BC,垂足为点N.
∴
| EM |
| DN |
| BE |
| BD |
| EM |
| AB |
| 2 |
| 3 |
而AB=12,
∴可求得EM=8.
∴S=
| 1 |
| 2 |
| 13 |
| 3 |
| 208 |
| 3 |

(3)作PH⊥BC,垂足为点H.
(i)当PQ=PG时,QH=GH=
| 13 |
| 2 |
∴2x+
| 13 |
| 2 |
解得x=
| 3 |
| 2 |
(ii)当PQ=GQ时,PQ=
| (11-3x)2+122 |
解得x=2或x=
| 16 |
| 3 |
综上所述,当△PQG是以PQ为腰的等腰三角形时,x的值为
| 3 |
| 2 |
| 16 |
| 3 |
点评:本题主要考查了平行线分线段成比例的性质以及梯形的面积的求解和等腰三角形的判定问题,能够利用所学知识熟练求解.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
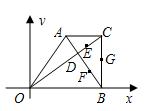 27、如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是( )
27、如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是( )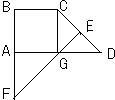 22、如图,已知在直角梯形ABCD中,BC∥AD,AB⊥AD,底AD=6,斜腰CD的垂直平分线EF交AD于G,交BA的延长线于F,且∠D=45°,求BF的长度.
22、如图,已知在直角梯形ABCD中,BC∥AD,AB⊥AD,底AD=6,斜腰CD的垂直平分线EF交AD于G,交BA的延长线于F,且∠D=45°,求BF的长度.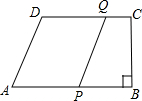 如图,已知在直角梯形ABCD中,AB∥CD,CD=9,∠B=90°,
如图,已知在直角梯形ABCD中,AB∥CD,CD=9,∠B=90°,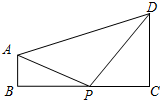 如图,已知在直角梯形ABCD中,AB∥CD,∠B=∠C=90°,AB=2,BC=7,CD=6,在BC上找一点P,使△ABP∽△DCP,求出BP的值.
如图,已知在直角梯形ABCD中,AB∥CD,∠B=∠C=90°,AB=2,BC=7,CD=6,在BC上找一点P,使△ABP∽△DCP,求出BP的值.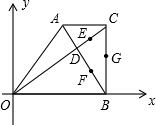 如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是点
如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是点