题目内容
16.若x1和x2分别是一元二次方程2x2+5x-3=0的两根.(1)求|x1-x2|的值;
(2)求$\frac{1}{{{x}_{1}}^{2}}$+$\frac{1}{{{x}_{2}}^{2}}$的值;
(3)x13+x23.
分析 (1)先利用根与系数的关系得到两根之和及两根之差,再对要求的代数式变形,把数值代入求解即可;
(2)先通分,再把分子利用完全平方公式变形,代入求得答案即可;
(3)利用立方和公式把代数式因式分解,再变形,再利用根与系数的关系即可求解.
解答 解:∵x1和x2分别是一元二次方程2x2+5x-3=0的两根.
∴x1+x2=-$\frac{5}{2}$,x1•x2=-$\frac{3}{2}$.
(1)|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{7}{2}$
(2)$\frac{1}{{{x}_{1}}^{2}}$+$\frac{1}{{{x}_{2}}^{2}}$
=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{{x}_{1}^{2}x}_{2}^{2}}$
=$\frac{37}{9}$
(3)x13+x23=(x1+x2)(x12-x1x2+x22)
=(x1+x2)[(x1+x2)2-3x1x2]
=-$\frac{5}{2}$×$\frac{43}{8}$
=-$\frac{215}{8}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
相关题目
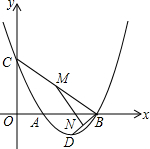 已知二次函数y=x2+bx+c,其图象交x轴于点A(1,0),B(3,0),交y轴于点C,点D为顶点.
已知二次函数y=x2+bx+c,其图象交x轴于点A(1,0),B(3,0),交y轴于点C,点D为顶点.