题目内容
15.如果有理数a,b满足|ab-2|+(1-b)2=0,试求$\frac{1}{ab}$+$\frac{1}{(a+1)(b+1)}$+$\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+2010)(b+2010)}$的值.分析 先利用非负数的性质求出a,b的值,再利用分式的规律化简求值即可.
解答 解:∵|ab-2|+(1-b)2=0,
∴ab-2=0,1-b=0,解得a=2,b=1,
∴$\frac{1}{ab}$+$\frac{1}{(a+1)(b+1)}$+$\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+2010)(b+2010)}$
=$\frac{1}{2×1}$+$\frac{1}{3×2}$+$\frac{1}{4×3}$+…+$\frac{1}{2012×2011}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…$\frac{1}{2011}$-$\frac{1}{2012}$
=1-$\frac{1}{2012}$
=$\frac{2011}{2012}$.
点评 本题主要考查了非负数的性质及分式的化简求值,解题的关键是能正确的找分式的规律.

练习册系列答案
相关题目
6.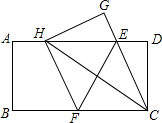 如图,在一张矩形纸片ABCD中,AB=2,BC=4,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,下列三个结论:①EF垂直平分HC;②EC平分∠DCH;③当点H与点A重合时,BF=$\frac{3}{2}$.其中正确的结论是( )
如图,在一张矩形纸片ABCD中,AB=2,BC=4,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,下列三个结论:①EF垂直平分HC;②EC平分∠DCH;③当点H与点A重合时,BF=$\frac{3}{2}$.其中正确的结论是( )
 如图,在一张矩形纸片ABCD中,AB=2,BC=4,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,下列三个结论:①EF垂直平分HC;②EC平分∠DCH;③当点H与点A重合时,BF=$\frac{3}{2}$.其中正确的结论是( )
如图,在一张矩形纸片ABCD中,AB=2,BC=4,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,下列三个结论:①EF垂直平分HC;②EC平分∠DCH;③当点H与点A重合时,BF=$\frac{3}{2}$.其中正确的结论是( )| A. | ①②③ | B. | ①② | C. | ②③ | D. | ①③ |
4.下列命题中,真命题是( )
| A. | 如果两个角相等,则这两个角是对顶角 | |
| B. | 三角形的角平分线是一条射线 | |
| C. | 互为邻补角的两个角相等 | |
| D. | 同角的余角相等 |
5.一个四边形,对于下列条件,不能判定为平行四边形的是( )
| A. | 对角线交点分别是两对角线的中点 | |
| B. | 一组对边平行,一组对角相等 | |
| C. | 一组对边相等,一条对角线被另一条对角线平分 | |
| D. | 一组对边平行,一条对角线被另一条对角线平分 |
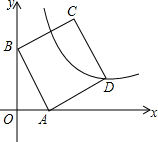 如图,在平面直角坐标系中,正方形ABCD的顶点A、B的坐标分别为A(1,0),B(0,2),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点D.
如图,在平面直角坐标系中,正方形ABCD的顶点A、B的坐标分别为A(1,0),B(0,2),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点D.