Question

11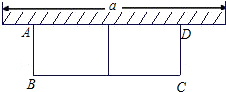．如图，要利用一面墙（墙的最大可用长度a为13m）建羊圈，用24米的围栏围成两个大小相同的矩形羊圈，设羊圈的宽AB为x（m），总面积为S（m²）．
（1）求S与x之间的函数关系式；
（2）如果要围成总面积为45m²的羊圈，AB的长是多少米？
（3）能围成总面积比45m²更大的羊圈吗？如果能，请求出最大总面积．并说明围法；如果不能，请说明理由．

Answer 1

分析 （1）根据长方形的面积公式可得；
（2）根据题意列出方程，解方程后根据墙的最大可用长度a为13m取舍可得；
（3）根据二次函数的性质求得最大值即可．

解答 解：（1）根据题意，得S=x（24-3x），
即所求的函数解析式为：S=-3x²+24x；

（2）根据题意，设AB长为x，则BC长为24-3x，
则-3x²+24x=45．
整理，得x²-8x+15=0，
解得x=3或5，
当x=3时，BC=24-9=15＞13不成立，
当x=5时，BC=24-15=9＜13成立，
∴AB长为5m；

（3）S=24x-3x²=-3（x-4）²+48
∵墙的最大可用长度为13m，
∴当x=4，有最大面积为48m²．
此时24-3x=12＜13
∴能围成最大面积为48m²的羊圈，其长和宽分别为12m、4m．

点评 本题主要考查二次函数的应用能力，根据题意找到长方形的长BC，并熟练掌握二次函数的性质是解题的关键．